9.4 *dres():观测方程的构建
本章节主要分析 zdres()、ddres() 和它们所调用的函数,其中部分内容与第 10 章的内容有所重复,因此这里不再赘述,例如 geodist(),satazel(),satexclude() 等函数。
其中的 varerr() 函数可以参考附录 C.3。
9.4.1 zdres():非差残差

图9.4-1 zdres() 函数调用
非差残差(Zero-Difference Residuals),相当于直接使用未做差的原始观测数据进行残差的计算。这里的残差可以简单的记作:OMC(Observation Minus Computed,观测值减去估计值),观测的估计量在整个过程中的修正包括潮汐修正(可选项)、卫星钟差修正、对流层修正,以及接收机天线偏移误差。
1. 参数列表
/* args */
int base I 0 表示接收机,1 表示基站
obsd_t *obs I obs观测数据
int n I obs的数量
double *rs I 卫星位置和速度,长度为 6*n,{x,y,z,vx,vy,vz}(ecef)(m,m/s)
double *dts I 卫星钟差,长度为 2*n, {bias,drift} (s|s/s)
int *svh I 卫星健康标志 (-1:correction not available)
nav_t *nav I NAV导航数据
double *rr I 接收机/基站的位置和速度,长度为 6*n,{x,y,z,vx,vy,vz}(ecef)(m,m/s)
prcopt_t *opt I 处理过程选项
int index I 0 表示接收机,1 表示基站,与参数 base 重复了
double *y O 相位/伪距残差
double *e O 观测矢量 (ecef)
double *azel O 方位角和俯仰角 (rad)
double *freq O 载波频率
/* return */
return status - 1 表示成功,0 表示失败2. 执行流程
- 初始化与检查:
- 将残差数组
y初始化为 0; - 若接收机位置
rr范数 <= 0,则返回 0。
- 将残差数组
- 位置修正:
- 复制接收机位置到
rr_; - 若启用潮汐修正(
opt->tidecorr),调用tidedisp进行地球潮汐修正(包括固体潮、极潮和海潮负荷)。
- 复制接收机位置到
- 坐标转换:
- 将 ECEF 坐标
rr_转换为大地坐标pos(经纬高)。
- 将 ECEF 坐标
- 卫星循环处理:
- 几何距离计算:调用
geodist()计算卫星到接收机的几何距离 r,并修正地球自转效应(Sagnac 效应)。 - 方位角/高度角:调用
satazel()计算azel,若高度角低于最小截止角opt->elmin,跳过该卫星。 - 卫星排除:调用
satexclude()检查卫星是否需排除(基于星历方差、健康状态等)。 - 钟差修正:用卫星钟差
dts修正几何距离 。 - 对流层延迟:调用
tropmapf()计算出干延迟投影系数(天顶方向到接收机相对卫星观测方向上的对流层延迟投影系数)。tropmodel()计算出的天顶对流层干延迟与tropmapf()计算出干延迟投影系数相乘,从而得到接收机相对卫星观测方向上的对流层延迟 ,对卫地距进行干延迟改正r+=tropmapf(obs[i].time,pos,azel+i*2,NULL)*zhd; - 天线偏移:调用
antmodel()计算接收机天线相位中心偏移dant,每一个频率都有一个值。相对定位只需要计算接收机端的天线相位中心修正值。因为相对定位进行单差时,已经将卫星端的天线误差消除了。
- 几何距离计算:调用
- 残差计算:
- 调用
zdres_sat()为每颗卫星计算非差相位和伪距残差:- 相位残差:
- 伪距残差:
- 其中 是载波相位观测量, 是伪距观测量, 是频率。
- 调用
- 调试输出:
- 记录位置、卫星信息和残差矩阵。
3. 注意事项
- 对流层修正:调用
tropmodel()利用 Saastamoinen 模型只改正对流层干延迟zhd(由于湿度值传 0,高度角传 0,只计算了天顶方向干延迟 ),湿分量会在之后的ddres()(双差残差)中进行扣除。 - 电离层修正:由于之后会计算双差后的残差,因此在短基线的情况下,大部分电离层误差已经得到了消除,所以未进行电离层误差修正;而对流层误差受基站和移动站之间的高度差影响,因此通常还需要进行考虑。
4. 源码注释
点击查看代码
/* undifferenced phase/code residuals ----------------------------------------
calculate zero diff residuals [observed pseudorange - range]
output is in y[0:nu-1], only shared input with base is nav
计算某历元可视卫星(未做差的)载波相位、伪距残差(残差 = 观测量 - 伪距估计量)
args: I base: 1=base,0=rover
I obs = sat observations
I n = # of sats
I rs [(0:2)+i*6]= sat position {x,y,z} (m)
I dts[(0:1)+i*2]= sat clock {bias,drift} (s|s/s)
I var = variance of ephemeris
I svh = sat health flags
I nav = sat nav data
I rr = rcvr pos (x,y,z)
I opt = options
O y[(0:1)+i*2] = zero diff residuals {phase,code} (m)
O e = line of sight unit vectors to sats
O azel = [az, el] to sats */
static int zdres(int base, const obsd_t *obs, int n, const double *rs,
const double *dts, const double *var, const int *svh,
const nav_t *nav, const double *rr, const prcopt_t *opt,
double *y, double *e, double *azel, double *freq)
{
double r, rr_[3], pos[3], dant[NFREQ] = {0}, disp[3]; /* 几何距离、接收机位置副本、大地坐标、天线偏移、潮汐位移 */
double mapfh, zhd, zazel[] = {0.0, 90.0 * D2R}; /* 对流层投影函数、水汽延迟、默认高度角 */
int i, nf = NF(opt); /* 循环索引、频率数 */
trace(3, "zdres : n=%d rr=%.2f %.2f %.2f\n", n, rr[0], rr[1], rr[2]); /* 调试:输出卫星数和接收机位置 */
/* 初始化残差为 0 */
for (i = 0; i < n * nf * 2; i++) y[i] = 0.0;
/* 若无接收机位置,直接返回 */
if (norm(rr, 3) <= 0.0) return 0;
/* 复制接收机位置 */
for (i = 0; i < 3; i++) rr_[i] = rr[i];
/* 进行地球潮汐修正(可选) */
if (opt->tidecorr) {
tidedisp(gpst2utc(obs[0].time), rr_, opt->tidecorr, &nav->erp, opt->odisp[base], disp);
for (i = 0; i < 3; i++) rr_[i] += disp[i]; /* 更新位置 */
}
/* ECEF 坐标转为大地坐标 */
ecef2pos(rr_, pos);
/* 遍历所有卫星 */
for (i = 0; i < n; i++) {
/* 计算几何距离和方位/高度角 */
if ((r = geodist(rs + i * 6, rr_, e + i * 3)) <= 0.0) continue; /* 几何距离 */
if (satazel(pos, e + i * 3, azel + i * 2) < opt->elmin) continue; /* 低于截止角跳过 */
/* 排除不可用卫星 */
if (satexclude(obs[i].sat, var[i], svh[i], opt)) continue;
/* 修正卫星钟差 */
r += -CLIGHT * dts[i * 2];
/* 修正对流层延迟 */
zhd = tropmodel(obs[0].time, pos, zazel, 0.0); /* 水汽延迟 */
mapfh = tropmapf(obs[i].time, pos, azel + i * 2, NULL); /* 投影函数 */
r += mapfh * zhd;
/* 计算接收机天线相位中心偏移 */
antmodel(opt->pcvr + base, opt->antdel[base], azel + i * 2, opt->posopt[1], dant);
/* 计算非差相位/伪距残差 */
trace(4, "sat=%d r=%.6f c*dts=%.6f zhd=%.6f map=%.6f\n", obs[i].sat, r, CLIGHT * dts[i * 2], zhd, mapfh);
zdres_sat(base, r, obs + i, nav, azel + i * 2, dant, opt, y + i * nf * 2, freq + i * nf);
}
trace(4, "rr_=%.3f %.3f %.3f\n", rr_[0], rr_[1], rr_[2]);
trace(4, "pos=%.9f %.9f %.3f\n", pos[0] * R2D, pos[1] * R2D, pos[2]);
for (i = 0; i < n; i++) {
if ((obs[i].L[0] == 0 && obs[i].L[1] == 0 && obs[i].L[2] == 0) || base == 0) continue;
trace(3, "sat=%2d rs=%13.3f %13.3f %13.3f dts=%13.10f az=%6.1f el=%5.1f\n",
obs[i].sat, rs[i * 6], rs[1 + i * 6], rs[2 + i * 6], dts[i * 2], azel[i * 2] * R2D, azel[1 + i * 2] * R2D);
}
trace(3, "y=\n"); tracemat(3, y, nf * 2, n, 13, 3);
return 1;
}9.4.2 ddres():计算双差残差、雅可比矩阵、新息向量

图9.4-2 ddres() 函数调用
ddres() 是构建相对定位观测方程最为重要的函数,因此本章将会增加一些篇幅进行描述。其构建了站星双差矩阵 v、双差雅可比矩阵 H,双差协方差矩阵 R。
1. 双差理论
该部分参考自资料[20]。
a. 单差、双差的概念
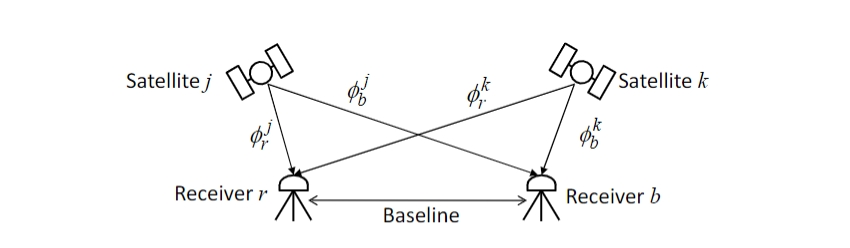
图9.4-3 双差模型
由于 GNSS 非差观测值中很多误差项具有很强的时空相关性,因此可以通过两台接收机的同步观测量或一台接收机的连续观测量求差来消除或减弱一些时空相关误差的影响,以达到减弱模型中未知参数个数和简化观测模型的目的。其中:
- 单差:在接收机间求一次差后,卫星星历误差、电离层延迟、对流层延迟误差等误差的影响也可得以消弱,在短基线定位中尤为明显。
- 双差:两颗卫星的单差观测量求差进一步得到双差观测量,由于接收机通道时延差异非常小,同一接收机相同历元的不同卫星观测量中相应的接收机钟差和接收机设备延迟可以认为相同的。因此,双差观测量可以进一步消除接收机钟差和接收机设备延迟误差,从而使双差模糊度可以进行有效分离,保留其整周特性。
b. 系统观测向量与观测方程
这里的 向量在 RTKLIB 中表示为 向量,向量其中:
- , 表示 i 频段的载波相位双差观测向量;
- ,表示 i 频段的伪距双差观测向量。
具体的双差模型为:
其中 表示双差几何距离, 表示频段 i 的波长, 表示单差模糊度(很多书籍中表示为 ,单位为cycle),在第一个方程中,第三项 为载波相位观测值改正项,短基线情况下可忽略。有关双差模型的更多描述可以参考书籍[4] 的8.3.5节。
c. 雅可比矩阵 H
同样根据双差模型的定义,可以得到:
从这里也可以看出,双差观测模型是一个非线性模型,其中:
那么:
则:
其中:
d. 观测噪声协方差阵 R
其中:
表示载波相位测量误差标准差, 表示伪距测量误差标准差。
中数值的含义?
表示载波相位测量误差标准差,我们将其简化为 ,我们认为流动站和基准站的标准差均为 。
现在我们需要求解载波相位单差标准差 和载波相位双差标准差 ,这里假设流动站和基准站的对同一颗卫星的测量误差一致。
如果不同卫星的单差测量误差也是一致的,那么同理可得 。
我们再回头看RTKLIB手册中的描述,载波相位单差的测量噪声 标准差可以表示为:
那么载波相位的双差测量噪声 标准差可以表示为:
则:
到这里已经得到了 RTKLIB 手册中的形态,假如不同接收机对同一颗卫星的载波相位测量噪声是一致的,并且不同卫星的单差测量噪声也是一致的,则:
相位单差标准差向量:
相位单差协方差矩阵:
相位双差协方差矩阵:
伪距的部分的测量噪声协方差矩阵同理可得。
2. 参数列表
/* args */
rtk_t *rtk IO rtk控制结构体
nav_t *nav I 导航数据
double dt I 接收机和基站的时间差
double *x IO 状态变量
double *P IO 状态变量的误差协方差阵
int sat I 接收机和基站共同观测的卫星号列表
double *y IO 相位/伪距残差
double *e IO 观测矢量 (ecef)
double *azel O 方位角和俯仰角 (rad)
int *iu I 接收机和基站共同观测的卫星在接收机观测值中的index值列表
int *ir I 接收机和基站共同观测的卫星在基站观测值中的index值列表
int ns I 接收机和基站共同观测的卫星个数
double *v O 实际观测量与预测观测量的残差(双差观测值新息向量)
double *R O 测量误差的协方差
double *H O 观测矩阵
int *vflg O 数据有效标志
/* return */
int nv - 有效数据数3. 执行流程
- 初始化:
- 计算基线长度
bl,基线向量dr; - 将 ECEF 坐标转换为大地坐标
posu(流动站)和posr(基站); - 初始化伪距残差
rtk->ssat[i].resp[j]、载波相位残差rtk->ssat[i].resc[j]为0 ; - 遍历所有共视卫星
- 计算基线长度
- 大气层延迟计算:
- 若启用电离层状态(
ionoopt == IONOOPT_EST),计算电离层映射函数平均值im[i]。 - 若启用对流层状态(
tropopt >= TROPOPT_EST),计算对流层延迟tropu[i]和tropr[i]及导数dtdxu,dtdxr。
- 若启用电离层状态(
- 星座系统和频率循环(若为
PMODE_DGPS模式,需限制遍历范围,0-nf为载波相位,nf-2nf为伪距):- 寻找仰角最高的卫星作为参考卫星;
- 为每个非参考卫星计算双差残差:
- 双差残差:([参考星(移动站) - 参考星(基准站)]-[非参考星(移动站) - 非参考星(基准站)]);
- 构建雅可比矩阵
H,移动站非参考星视线向量 - 移动站参考星视线向量(视线差)。
- 误差调整:
- 电离层延迟:, 赋值相应项。
- 对流层延迟:, 赋值导数。
- 相位偏移:若非 IFLC,, 赋值(用单差模糊度参数修正
v和H)。 - GLONASS/SBAS 调整:处理频率差或 IC 偏差。
- 残差存储与异常检测:
- 将残差存入
resp(伪距)或resc(相位)。 - 检查残差是否超出阈值(
opt->maxinno),若超出标记为异常。
- 将残差存入
- 噪声协方差:
- 调用
varerr计算单差噪声Ri,Rj,调整半周偏差。 - 调用
ddcov构建双差噪声协方差 。
- 调用
- 基线约束:
- 若启用基线长度约束,调用
constbl添加约束项。
- 若启用基线长度约束,调用
4. 注意事项
- RTKLIB 的卡尔曼滤波步骤与传统方法不同:
- 传统方法先计算一步预测 ,再减去观测值得到残差;
- RTKLIB 则先通过
zdres()计算非差残差(观测量-预测值),然后在ddres()中计算双差残差,两者是等价的。
ddres()仅扣除对流层湿分量延迟,干分量已在zdres()中处理。
5. 源码注释
点击查看代码
/* double-differenced residuals and partial derivatives -----------------------------------
O rtk->ssat[i].resp[j] = residual pseudorange error
O rtk->ssat[i].resc[j] = residual carrier phase error
I rtk->rb= base location
I dt = time diff between base and rover observations
I x = rover pos & vel and sat phase biases (float solution)
I P = error covariance matrix of float states
I sat = list of common sats
I y = zero diff residuals (code and phase, base and rover)
I e = line of sight unit vectors to sats
I azel = [az, el] to sats
I iu,ir = user and ref indices to sats
I ns = # of sats
O v = double diff innovations (measurement-model) (phase and code)
O H = linearized translation from innovations to states (az/el to sats)
O R = measurement error covariances
O vflg = bit encoded list of sats used for each double diff */
static int ddres(rtk_t *rtk, const obsd_t *obs, double dt, const double *x,
const double *P, const int *sat, double *y, double *e,
double *azel, double *freq, const int *iu, const int *ir,
int ns, double *v, double *H, double *R, int *vflg)
{
prcopt_t *opt = &rtk->opt; /* 解算选项 */
double bl, dr[3], posu[3], posr[3], didxi = 0.0, didxj = 0.0, *im, threshadj; /* 基线长度、位移分量、大地坐标、电离层延迟、阈值调整 */
double *tropr, *tropu, *dtdxr, *dtdxu, *Ri, *Rj, freqi, freqj, *Hi = NULL, df; /* 延迟和导数、噪声、频率、量测矩阵指针 */
int i, j, k, m, f, nv = 0, nb[NFREQ * NSYS * 2 + 2] = {0}, b = 0, sysi, sysj, nf = NF(opt); /* 索引、计数器 */
int ii, jj, frq, code;
trace(3, "ddres : dt=%.4f ns=%d\n", dt, ns); /* 调试:输出时间差和卫星数 */
/* 计算基线长度 bl 和分量 dr */
bl = baseline(x, rtk->rb, dr);
/* 转换为大地坐标:流动站 posu,基站 posr */
ecef2pos(x, posu); ecef2pos(rtk->rb, posr);
Ri = mat(ns * nf * 2 + 2, 1); Rj = mat(ns * nf * 2 + 2, 1); im = mat(ns, 1); /* 分配矩阵 */
tropu = mat(ns, 1); tropr = mat(ns, 1); dtdxu = mat(ns, 3); dtdxr = mat(ns, 3);
/* 初始化所有卫星的伪距残差 resp 和载波相位残差 resc 为 0 */
for (i = 0; i < MAXSAT; i++) for (j = 0; j < NFREQ; j++) {
rtk->ssat[i].resp[j] = rtk->ssat[i].resc[j] = 0.0;
}
/* 计算电离层和对流层延迟因子 */
for (i = 0; i < ns; i++) {
/* 若电离层模式 >= IONOOPT_EST,计算电离层延迟因子平均值 */
if (opt->ionoopt >= IONOOPT_EST) {
im[i] = (ionmapf(posu, azel + iu[i] * 2) + ionmapf(posr, azel + ir[i] * 2)) / 2.0;
}
/* 若对流层模式 >= TROPOPT_EST,计算对流层延迟因子 */
if (opt->tropopt >= TROPOPT_EST) {
tropu[i] = prectrop(rtk->sol.time, posu, 0, azel + iu[i] * 2, opt, x, dtdxu + i * 3);
tropr[i] = prectrop(rtk->sol.time, posr, 1, azel + ir[i] * 2, opt, x, dtdxr + i * 3);
}
}
/* 遍历不同系统:m=0:GPS/SBS, 1:GLO, 2:GAL, 3:BDS, 4:QZS, 5:IRN */
for (m = 0; m < 6; m++) {
/* 遍历每个频率,计算双差残差 */
/* 若为 PMODE_DGPS 伪距双差,限制范围;载波相位 0-nf,伪距 nf-2nf */
for (f = opt->mode > PMODE_DGPS ? 0 : nf; f < nf * 2; f++) {
frq = f % nf; code = f < nf ? 0 : 1; /* 频率和类型 */
/* 寻找仰角最高的卫星作为参考卫星 */
for (i = -1, j = 0; j < ns; j++) {
sysi = rtk->ssat[sat[j] - 1].sys;
if (!test_sys(sysi, m)) continue;
if (!validobs(iu[j], ir[j], f, nf, y)) continue;
if (i < 0 || azel[1 + iu[j] * 2] >= azel[1 + iu[i] * 2]) i = j;
}
if (i < 0) continue; /* 选取失败则继续 */
/* 遍历所有卫星,计算双差 */
for (j = 0; j < ns; j++) {
if (i == j) continue; /* 跳过参考卫星 */
sysi = rtk->ssat[sat[i] - 1].sys;
sysj = rtk->ssat[sat[j] - 1].sys;
freqi = freq[frq + iu[i] * nf];
freqj = freq[frq + iu[j] * nf];
if (!test_sys(sysj, m)) continue;
if (!validobs(iu[j], ir[j], f, nf, y)) continue;
/* 使用非差残差 y 计算双差残差 v,并初始化 H 矩阵 */
if (H) {
Hi = H + nv * rtk->nx;
for (k = 0; k < rtk->nx; k++) Hi[k] = 0.0;
}
/* 双差残差:【参考星(移动站) - 参考星(基准站)】 - 【非参考星(移动站) - 非参考星(基准站)】 */
v[nv] = (y[f + iu[i] * nf * 2] - y[f + ir[i] * nf * 2]) -
(y[f + iu[j] * nf * 2] - y[f + ir[j] * nf * 2]);
/* 移动站位置偏导:非参考星视线向量 - 参考星视线向量 */
if (H) {
for (k = 0; k < 3; k++) {
Hi[k] = -e[k + iu[i] * 3] + e[k + iu[j] * 3]; /* 每行前 3 列为观测向量差 */
}
}
/* 电离层延迟调整:注意伪距和载波相位符号相反 */
if (opt->ionoopt == IONOOPT_EST) {
didxi = (f < nf ? -1.0 : 1.0) * im[i] * SQR(FREQ1 / freqi); /* 载波为负 */
didxj = (f < nf ? -1.0 : 1.0) * im[j] * SQR(FREQ1 / freqj); /* 伪距为正 */
v[nv] -= didxi * x[II(sat[i], opt)] - didxj * x[II(sat[j], opt)];
if (H) {
Hi[II(sat[i], opt)] = didxi;
Hi[II(sat[j], opt)] = -didxj;
}
}
/* 对流层延迟调整 */
if (opt->tropopt == TROPOPT_EST || opt->tropopt == TROPOPT_ESTG) {
v[nv] -= (tropu[i] - tropu[j]) - (tropr[i] - tropr[j]);
for (k = 0; k < (opt->tropopt < TROPOPT_ESTG ? 1 : 3); k++) {
if (!H) continue;
Hi[IT(0, opt) + k] = (dtdxu[k + i * 3] - dtdxu[k + j * 3]);
Hi[IT(1, opt) + k] = -(dtdxr[k + i * 3] - dtdxr[k + j * 3]);
}
}
/* 相位偏移调整:非 IFLC 模式扣除双差模糊度 */
if (f < nf) {
if (opt->ionoopt != IONOOPT_IFLC) {
v[nv] -= CLIGHT / freqi * x[IB(sat[i], f, opt)] -
CLIGHT / freqj * x[IB(sat[j], f, opt)];
if (H) {
Hi[IB(sat[i], f, opt)] = CLIGHT / freqi;
Hi[IB(sat[j], f, opt)] = -CLIGHT / freqj;
}
} else {
v[nv] -= x[IB(sat[i], f, opt)] - x[IB(sat[j], f, opt)];
if (H) {
Hi[IB(sat[i], f, opt)] = 1.0;
Hi[IB(sat[j], f, opt)] = -1.0;
}
}
}
/* 输出双差残差到相应结构体 */
if (f < nf) rtk->ssat[sat[j] - 1].resc[f] = v[nv]; /* 载波相位 */
else rtk->ssat[sat[j] - 1].resp[f - nf] = v[nv]; /* 伪距 */
/* 检测异常:根据 maxinno 排除数据 */
if (opt->maxinno > 0.0 && fabs(v[nv]) > opt->maxinno) {
if (f < nf) {
rtk->ssat[sat[i] - 1].rejc[f]++;
rtk->ssat[sat[j] - 1].rejc[f]++;
}
errmsg(rtk, "outlier rejected (sat=%3d-%3d %s%d v=%.3f)\n",
sat[i], sat[j], f < nf ? "L" : "P", f % nf + 1, v[nv]);
continue;
}
/* 计算单差测量误差协方差 */
Ri[nv] = varerr(sat[i], sysi, azel[1 + iu[i] * 2], bl, dt, f, opt);
Rj[nv] = varerr(sat[j], sysj, azel[1 + iu[j] * 2], bl, dt, f, opt);
/* 设置数据有效标志 */
if (opt->mode > PMODE_DGPS) {
if (f < nf) rtk->ssat[sat[i] - 1].vsat[f] = rtk->ssat[sat[j] - 1].vsat[f] = 1;
} else {
rtk->ssat[sat[i] - 1].vsat[f - nf] = rtk->ssat[sat[j] - 1].vsat[f - nf] = 1;
}
trace(4, "sat=%3d-%3d %s%d v=%13.3f R=%8.6f %8.6f\n", sat[i],
sat[j], f < nf ? "L" : "P", f % nf + 1, v[nv], Ri[nv], Rj[nv]);
vflg[nv++] = (sat[i] << 16) | (sat[j] << 8) | ((f < nf ? 0 : 1) << 4) | (f % nf);
nb[b]++;
}
b++;
}
}
/* 动基线模式添加基线长度约束 */
if (opt->mode == PMODE_MOVEB && constbl(rtk, x, P, v, H, Ri, Rj, nv)) {
vflg[nv++] = 3 << 4;
nb[b++]++;
}
if (H) { trace(5, "H=\n"); tracemat(5, H, rtk->nx, nv, 7, 4); }
/* 计算双差量测噪声协方差矩阵 R */
ddcov(nb, b, Ri, Rj, nv, R);
free(Ri); free(Rj); free(im); /* 释放内存 */
free(tropu); free(tropr); free(dtdxu); free(dtdxr);
return nv; /* 返回有效量测数 */
}9.4.3 tidedisp():地球潮汐校正
tidedisp() 函数是 RTKLIB 中用于计算地球潮汐引起的位移(displacement)的函数,主要用于修正 GNSS 观测中的潮汐效应。地球潮汐包括固体潮、海洋潮汐负荷和极潮(pole tide),这些效应会影响接收机和卫星的相对位置。
1. 参数列表
/* args */
gtime_t tutc I UTC时间
double *rr I 站点位置(地心地固坐标系,单位:米)
int opt I 选项(以下选项的按位或)
1: 固体潮
2: 海潮负荷
4: 极潮
8: 消除永久形变
double *erp I 地球自转参数(NULL:不使用)
double *odisp I 海潮负荷参数(NULL:不使用)
odisp[0+i*6]: 第i个分潮的径向振幅(米)
odisp[1+i*6]: 第i个分潮的向西振幅(米)
odisp[2+i*6]: 第i个分潮的向南振幅(米)
odisp[3+i*6]: 第i个分潮的径向相位(度)
odisp[4+i*6]: 第i个分潮的向西相位(度)
odisp[5+i*6]: 第i个分潮的向南相位(度)
(i=0:M2,1:S2,2:N2,3:K2,4:K1,5:O1,6:P1,7:Q1,
8:Mf,9:Mm,10:Ssa)
double *dr O 地球潮汐引起的位移(地心地固坐标系,单位:米)
/* return */
none2. 执行流程
- 潮汐类型:
- 固体潮:由太阳和月球引力引起的地壳变形。
- 海洋潮汐负荷:海洋潮汐引起的地面形变。
- 极潮:由于地球自转轴的极移导致的位移。
- 计算流程:
- 根据输入时间和地球自转参数调整为 GPST 时间。
- 将 ECEF 坐标转换为地心纬度和经度。
- 根据选项计算各潮汐分量,转换为 ECEF 坐标系。
- 累加各分量位移到
dr。
3. 源码注释
点击查看代码
/* tidal displacement: displacements by earth tides */
extern void tidedisp(gtime_t tutc, const double *rr, int opt, const erp_t *erp,
const double *odisp, double *dr)
{
gtime_t tut; /* 调整后的 GPST 时间 */
double pos[2], E[9], drt[3], denu[3], rs[3], rm[3], gmst, erpv[5] = {0}; /* 地心坐标、转换矩阵、位移、太阳/月球位置、GMST、ERP 参数 */
int i;
#ifdef IERS_MODEL
double ep[6], fhr; /* 历元和小时 */
int year, mon, day;
#endif
trace(3, "tidedisp: tutc=%s\n", time_str(tutc, 0)); /* 调试:输出 UTC 时间 */
/* 获取地球自转参数 */
if (erp) {
geterp(erp, utc2gpst(tutc), erpv);
}
tut = timeadd(tutc, erpv[2]); /* 调整为 GPST 时间 */
dr[0] = dr[1] = dr[2] = 0.0; /* 初始化位移为 0 */
/* 检查接收机位置有效性 */
if (norm(rr, 3) <= 0.0) return;
/* 计算地心纬度和经度 */
pos[0] = asin(rr[2] / norm(rr, 3)); /* 纬度 */
pos[1] = atan2(rr[1], rr[0]); /* 经度 */
xyz2enu(pos, E); /* 生成 ENU 到 ECEF 转换矩阵 */
/* 固体潮计算 */
if (opt & 1) { /* 固体潮 */
/* 获取太阳和月球位置 */
sunmoonpos(tutc, erpv, rs, rm, &gmst);
#ifdef IERS_MODEL
time2epoch(tutc, ep); /* 转换为历元 */
year = (int)ep[0]; mon = (int)ep[1]; day = (int)ep[2];
fhr = ep[3] + ep[4] / 60.0 + ep[5] / 3600.0; /* 小时 */
/* 调用 IERS 模型 */
dehanttideinel_((double *)rr, &year, &mon, &day, &fhr, rs, rm, drt);
#else
tide_solid(rs, rm, pos, E, gmst, opt, drt); /* 近似计算 */
#endif
for (i = 0; i < 3; i++) dr[i] += drt[i]; /* 累加位移 */
}
/* 海洋潮汐负荷 */
if ((opt & 2) && odisp) {
tide_oload(tut, odisp, denu); /* 计算 ENU 位移 */
matmul("TN", 3, 1, 3, E, denu, drt); /* 转换为 ECEF */
for (i = 0; i < 3; i++) dr[i] += drt[i];
}
/* 极潮 */
if ((opt & 4) && erp) {
tide_pole(tut, pos, erpv, denu); /* 计算 ENU 位移 */
matmul("TN", 3, 1, 3, E, denu, drt); /* 转换为 ECEF */
for (i = 0; i < 3; i++) dr[i] += drt[i];
}
trace(5, "tidedisp: dr=%.3f %.3f %.3f\n", dr[0], dr[1], dr[2]); /* 调试:输出总位移 */
}9.4.4 tropmodel():计算对流层延迟
通过标准大气模型和saastamoinen模型计算对流层延迟(m),该部分可以参考 RTKLIB-Manual-CN E.5节
1. 参数列表
/* args */
gtime_t time I time
double *pos I receiver position {lat,lon,h} (rad,m)
double *azel I azimuth/elevation angle {az,el} (rad)
double humi I relative humidity
/* return */
double delay - tropospheric delay (m)2. 执行流程
- 输入检查:
- 若 pos[2] < -100.0 或 > 1E4 或 azel[1] <= 0,返回 0(表示无效输入)。
- 标准大气参数计算:
- hgt:高度取正值(负值设为 0)。
- pres:大气压力,公式为 (单位:hPa)。
- temp:温度,公式为 (单位:K)。
- e:水汽压,公式为 (单位:hPa)。
- Saastamoinen 模型计算:
- z: zenith 角,(rad)。
- trph:干分量延迟,公式为 (单位:m)。
- trpw:湿分量延迟,公式为 (单位:m)。 总延迟:。
3. 注意事项
- 该函数计算静力学延迟和湿延迟时所使用的公式和 manual 手册上不一致。但代码并没有错误,代码中使用的是正确的 Saastamoinen 模型公式:
- 可参考这篇博客。最原始的 Saastamoinen 的论文《Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites》由于找到的下载网站都需要收费,所以我参考了另一篇SCI论文《A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region》,也和代码中公式一致。

- 《GPS测量与数据处理》第三版中是乘以(1.0-0.00266cos(2.0pos[0])-0.00028*hgt/1E3),而不是除以。我感觉可能是书中的书写错误,大部分文献中还是用的除以。
- Saastamoinen 模型公式貌似也有很多变形和近似,就没有再进行深入研究了。
- 可参考这篇博客。最原始的 Saastamoinen 的论文《Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites》由于找到的下载网站都需要收费,所以我参考了另一篇SCI论文《A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region》,也和代码中公式一致。
- 在 zdres 中使用该函数时,传入参数 azel[]={0.0,90.0*D2R},humi 为 0,因此实际上求取的是天顶方向的干延迟,接下来的tropmapf 函数将计算天顶方向到观测方向的对流层延迟投影函数。
4. 源码注释
点击查看代码
/* troposphere model -----------------------------------------------------------
* compute tropospheric delay by standard atmosphere and saastamoinen model
* args : gtime_t time I time
* double *pos I receiver position {lat,lon,h} (rad,m)
* double *azel I azimuth/elevation angle {az,el} (rad)
* double humi I relative humidity
* return : tropospheric delay (m)
*-----------------------------------------------------------------------------*/
extern double tropmodel(gtime_t time, const double *pos, const double *azel,
double humi)
{
const double temp0 = 15.0; /* 海平面温度 (单位:℃) */
double hgt, pres, temp, e, z, trph, trpw; /* 高度、大气压力、温度、水汽压、zenith角、干/湿延迟 */
/* 检查输入有效性:高度 -100m 至 10000m,高度角 > 0 */
if (pos[2] < -100.0 || 1E4 < pos[2] || azel[1] <= 0) return 0.0;
/* 标准大气模型 */
hgt = pos[2] < 0.0 ? 0.0 : pos[2]; /* 高度取正值 */
pres = 1013.25 * pow(1.0 - 2.2557E-5 * hgt, 5.2568); /* 大气压力 (hPa) */
temp = temp0 - 6.5E-3 * hgt + 273.16; /* 温度 (K) */
e = 6.108 * humi * exp((17.15 * temp - 4684.0) / (temp - 38.45)); /* 水汽压 (hPa) */
/* Saastamoinen 模型 */
z = PI / 2.0 - azel[1]; /* zenith 角 */
trph = 0.0022768 * pres / (1.0 - 0.00266 * cos(2.0 * pos[0]) - 0.00028 * hgt / 1E3) / cos(z); /* 干分量延迟 (m) */
trpw = 0.002277 * (1255.0 / temp + 0.05) * e / cos(z); /* 湿分量延迟 (m) */
return trph + trpw; /* 返回总延迟 (m) */
}9.4.5 tropmapf():计算对流程延迟投影
tropmapf() 函数是 RTKLIB 中用于计算对流层映射函数(tropospheric mapping function)的函数,基于 Niell Mapping Function (NMF) 或 Global Mapping Function (GMF)。映射函数用于将对流层延迟从 zenith 方向投影到任意 elevation 角方向,是 GNSS 观测数据校正中的关键步骤。
1. 参数列表
/* args */
gtime_t t I time
double *pos I receiver position {lat,lon,h} (rad,m)
double *azel I azimuth/elevation angle {az,el} (rad)
double *mapfw IO wet mapping function (NULL: not output)
/* return */
double nmf - dry mapping function2. 执行流程
- 输入检查与调试:
- 检查高度 pos[2] 是否在 -1000 米至 20,000 米范围内,若超出返回 0。
- 输出调试信息(位置和角度转为度)。
- IERS_MODEL 模式(GMF):
- GMF 模型:
- (干分量)。
- (湿分量)。
- 若定义了 IERS_MODEL:
- 计算修正儒略日 mjd(从 2000-01-01 12:00 UTC 开始)。
- 提取纬度 lat、经度 lon,并调整高度 hgt(减去大地水准面高度)。
- 计算 zenith 距离 zd = \pi/2 - azel[1]。
- 调用 gmf_ 函数计算干映射函数 gmfh 和湿映射函数 gmfw。
- 返回 gmfh,并将 gmfw 赋值给 mapfw(若非 NULL)。
- GMF 模型:
- 默认模式(NMF):
- NMF 模型:
- 。
- 若未定义 IERS_MODEL,调用 nmf 函数计算映射函数。
- 返回干分量映射函数,并更新 mapfw(若非 NULL)。
- NMF 模型:
3. 注意事项
- 干投影函数是通过返回值获得的,而湿投影是通过输入/输出参数mapfw获得的。在zdres函数中,本函数输入的mapfw=NULL,即不输出湿投影。
- NMF:基于经验公式,适用于一般情况;GMF:基于 IERS 模型,考虑时间和地理位置的季节性变化。
- 这个函数中有两种投影函数的计算方法,分别是 GMF 和 NMF,对应的两篇参考论文为“Global mapping functions for the atmosphere delay at radio wavelengths”和“Global Mapping Function(GMF): A new empirical mapping function base on numerical weather model data”。默认使用的是NMF方法,也可以通过定义IERS_MODEL宏来使用GMF方法。
- 这个函数调用完成后,会将返回的干投影函数和tropmodel中计算得到的天顶方向对流层干延迟相乘,从而得到接收机相对卫星观测方向上的对流层延迟。
4. 问题解答
- zdres函数调用这个函数时,为什么仅计算干延迟的投影函数?因为干延迟占延迟总量的90%,所以湿延迟忽略不计了吗?
5. 源码注释
点击查看代码
/* troposphere mapping function ------------------------------------------------
* compute tropospheric mapping function by NMF
* args : gtime_t t I time
* double *pos I receiver position {lat,lon,h} (rad,m)
* double *azel I azimuth/elevation angle {az,el} (rad)
* double *mapfw IO wet mapping function (NULL: not output)
* return : dry mapping function
* note : see ref [5] (NMF) and [9] (GMF)
* original JGR paper of [5] has bugs in eq.(4) and (5). the corrected
* paper is obtained from:
* ftp://web.haystack.edu/pub/aen/nmf/NMF_JGR.pdf
*-----------------------------------------------------------------------------*/
extern double tropmapf(gtime_t time, const double pos[], const double azel[],
double *mapfw)
{
#ifdef IERS_MODEL
const double ep[] = {2000, 1, 1, 12, 0, 0}; /* 参考时间 2000-01-01 12:00 UTC */
double mjd, lat, lon, hgt, zd, gmfh, gmfw; /* 修正儒略日、纬度、经度、调整高度、zenith距离、干/湿映射函数 */
#endif
trace(4, "tropmapf: pos=%10.6f %11.6f %6.1f azel=%5.1f %4.1f\n",
pos[0] * R2D, pos[1] * R2D, pos[2], azel[0] * R2D, azel[1] * R2D); /* 调试:输出位置 (度) 和角度 (度) */
/* 检查高度范围:-1000m 至 20000m */
if (pos[2] < -1000.0 || pos[2] > 20000.0) {
if (mapfw) *mapfw = 0.0; /* 无效时清零湿映射函数 */
return 0.0; /* 无效时返回 0 */
}
#ifdef IERS_MODEL
/* 计算修正儒略日(从 2000-01-01 12:00 UTC 开始) */
mjd = 51544.5 + (timediff(time, epoch2time(ep))) / 86400.0;
lat = pos[0]; /* 纬度 (弧度) */
lon = pos[1]; /* 经度 (弧度) */
hgt = pos[2] - geoidh(pos); /* 调整高度(海平面高度,单位:米) */
zd = PI / 2.0 - azel[1]; /* zenith 距离 (弧度) */
/* 调用 GMF 模型计算干/湿映射函数 */
gmf_(&mjd, &lat, &lon, &hgt, &zd, &gmfh, &gmfw);
if (mapfw) *mapfw = gmfw; /* 输出湿映射函数 */
return gmfh; /* 返回干映射函数 */
#else
return nmf(time, pos, azel, mapfw); /* 默认使用 NMF 模型 */
#endif
}9.4.6 antmodel():计算天线偏移量
根据接收机天线的相位中心参数计算天线偏移量,注意当前版本不支持方位依赖项(azimuth dependent terms)。
1. 参数列表
/* args */
pcv_t *pcv I antenna phase center parameters
double *del I 配置中所设置天线参考点(ARP)相对于地面标识的偏移
double *azel I azimuth/elevation for receiver {az,el} (rad)
int opt I option (0:only offset,1:offset+pcv)
double *dant O range offsets for each frequency (m)
/* return */2. 执行流程
- 调试与初始化:
- 输出调试信息(方位角、高度角和选项)。
- 计算视线单位向量 e:
- $ e[0] = \sin(az) \cdot \cos(el) $(东向分量)。
- $ e[1] = \cos(az) \cdot \cos(el) $(北向分量)。
- $ e[2] = \sin(el) $(上向分量)。
- 偏移计算循环:
- 遍历每个频率 i(NFREQ 定义的频率数):
- 计算总偏移 off[j]:$ off[j] = pcv->off[i][j] + del[j] $(j = 0, 1, 2 对应 e, n, u)。
- 计算范围偏移 dant[i]:
- 投影偏移到视线方向:$ - \text{dot3}(off, e) $(负号表示从相位中心到天线参考点的方向)。
- 若 opt == 1,添加相位中心变差:$ + \text{interpvar}(90 - el \cdot R2D, pcv->var[i]) $(elevation 角转为度后插值)。 注意:频段不同,天线的相位中心偏移(PCO)不同;而高度角不同,天线相位中心变化量(PCV)也不同。
- 遍历每个频率 i(NFREQ 定义的频率数):
- 调试输出:
- 输出前两个频率的 dant 值。
3. 注意事项
- 天线偏移量总共包括了三部分:a) 天线相位偏移(PCO) ARP –> APC(天线参考点到天线平均相位中心)b) 天线相位变化(PCV) APC –> IPC(平均相位中心到瞬时相位中心)c) 天线参考点(ARP)相对于地面标识的偏移
- 相位中心偏移pcv->off[i][j]中的值来自于天线PCV文件。另外我在理解该函数的过程中,也看到另外两篇博客(博客1,博客2)对RTKlib中的天线偏移有所解释,如果不理解可以作为辅助阅读。
4. 源码注释
点击查看代码
/* receiver antenna model ------------------------------------------------------
* compute antenna offset by antenna phase center parameters
* args : pcv_t *pcv I antenna phase center parameters
* double *del I antenna delta {e,n,u} (m)
* double *azel I azimuth/elevation for receiver {az,el} (rad)
* int opt I option (0:only offset,1:offset+pcv)
* double *dant O range offsets for each frequency (m)
* return : none
* notes : current version does not support azimuth dependent terms
*-----------------------------------------------------------------------------*/
extern void antmodel(const pcv_t *pcv, const double *del, const double *azel,
int opt, double *dant)
{
double e[3], off[3], cosel = cos(azel[1]); /* 视线单位向量、总偏移、cos(el) */
int i, j;
trace(4, "antmodel: azel=%6.1f %4.1f opt=%d\n", azel[0] * R2D, azel[1] * R2D, opt); /* 调试:输出方位角 (度)、高度角 (度) 和选项 */
/* 构造视线单位向量 */
e[0] = sin(azel[0]) * cosel; /* 东向分量 */
e[1] = cos(azel[0]) * cosel; /* 北向分量 */
e[2] = sin(azel[1]); /* 上向分量 */
/* 遍历每个频率,计算范围偏移 */
for (i = 0; i < NFREQ; i++) {
/* 计算总偏移:相位中心偏移 + 安装偏移 */
for (j = 0; j < 3; j++) off[j] = pcv->off[i][j] + del[j];
/* 计算范围偏移:投影到视线方向,添加变差 (若 opt=1) */
dant[i] = -dot3(off, e) + (opt ? interpvar(90.0 - azel[1] * R2D, pcv->var[i]) : 0.0);
}
trace(4, "antmodel: dant=%6.3f %6.3f\n", dant[0], dant[1]); /* 调试:输出前两个频率的偏移 */
}9.4.7 zdres_sat():计算一个站心非差残差
计算接收机或基站对某一颗卫星的非差残差,在此实现无电离层组合。
1. 参数列表:
/* args */
int base I 0 表示接收机,1 表示基站
double r I 经过钟差和对流层校正后的几何距离
obsd_t *obs I obs观测数据
nav_t *nav I NAV导航数据
double *azel I 方位角和俯仰角 (rad)
double *dant I 接收机天线校正值
prcopt_t *opt I 处理过程选项
double *y O 非差闭合差
double *freq O 载波频率
/* return */
none2. 执行流程:
- 如果是无电离层组合
IONOOPT_IFLC:- 调用
sat2freq()获取观测值obs->code[0]、obs->code[1]的频率freq1、freq2; - 调用
testsnr()检测信噪比是否都小于opt->snrmask; - 计算无电离层组合系数
c1、c2; - 计算天线校正值
dant_if; - 计算载波相位残差
y[0],伪距残差y[1],残差 = IFLC观测量 - 卫地距 - 天线偏移量;其中 消除电离层效应。 freq[0]=1.0。
- 调用
- 不是无电离层组合的情况,for循环遍历
obs所有频率值,都计算残差:- 调用
sat2freq()获取obs->code[i]频率freq[i]; - 调用
testsnr()检测信噪比是否小于opt->snrmask; - 计算载波相位残差
y[i],伪距残差y[i+nf],残差 = 观测量 - 卫地距 - 天线偏移量
- 调用
3. 注意事项
- 无电离层组合:无电离层组合消除了电离层一阶项的影响,但模糊度不再为整数,且其组合的观测噪声放大了 3 倍(参考附录 B.4)。在短基线计算时,由于电离层影响很小,即使具有双频观测值,仍采用 L1 载波观测值进行解算。但是对于长基线,电离层误差是不可以忽略的误差源,故采用无电离层组合观测值进行计算,以保证定位精度。
4. 源码注释
点击查看代码
static void zdres_sat(int base, double r, const obsd_t *obs, const nav_t *nav,
const double *azel, const double *dant,
const prcopt_t *opt, double *y, double *freq)
{
double freq1,freq2,C1,C2,dant_if;
int i,nf=NF(opt);
// 电离层校正模式为 IONOOPT_IFLC 的情况
if (opt->ionoopt==IONOOPT_IFLC) { /* iono-free linear combination */
// 获取观测值 obs->code[0]、obs->code[1] 的频率 freq1、freq2
freq1=sat2freq(obs->sat,obs->code[0],nav);
freq2=sat2freq(obs->sat,obs->code[1],nav);
if (freq1==0.0||freq2==0.0) return;
// 检测信噪比
if (testsnr(base,0,azel[1],obs->SNR[0]*SNR_UNIT,&opt->snrmask)||
testsnr(base,1,azel[1],obs->SNR[1]*SNR_UNIT,&opt->snrmask)) return;
// 计算无电离层组合系数c1、c2 (E.5.23)
C1= SQR(freq1)/(SQR(freq1)-SQR(freq2));
C2=-SQR(freq2)/(SQR(freq1)-SQR(freq2));
// 计算天线校正值 dant_if
dant_if=C1*dant[0]+C2*dant[1];
// 计算残差,残差 = IFLC观测量 - 卫地距 - 天线偏移量
if (obs->L[0]!=0.0&&obs->L[1]!=0.0) { // 载波相位残差 (E.5.22)
y[0]=C1*obs->L[0]*CLIGHT/freq1+C2*obs->L[1]*CLIGHT/freq2-r-dant_if;
}
if (obs->P[0]!=0.0&&obs->P[1]!=0.0) { // 伪距残差 (E.5.21)
y[1]=C1*obs->P[0]+C2*obs->P[1]-r-dant_if;
}
freq[0]=1.0;
}
// 电离层校正模式不为 IONOOPT_IFLC 的情况
else {
for (i=0;i<nf;i++) {
if ((freq[i]=sat2freq(obs->sat,obs->code[i],nav))==0.0) continue;
// 检测信噪比
/* check SNR mask */
if (testsnr(base,i,azel[1],obs->SNR[i]*SNR_UNIT,&opt->snrmask)) {
continue;
}
// 计算残差,残差 = IFLC观测量 - 卫地距 - 天线偏移量
/* residuals = observable - pseudorange */
if (obs->L[i]!=0.0) y[i ]=obs->L[i]*CLIGHT/freq[i]-r-dant[i];
if (obs->P[i]!=0.0) y[i+nf]=obs->P[i] -r-dant[i];
}
}
}9.4.8 ionmapf():SLM(Single-Layer Model)投影映射模型
这部分对应的公式在 RTKLIB-Manual-CN E.5节电离层模型部分。本函数实际是在计算电离层延迟的投影系数,即 。
1. 原理分析
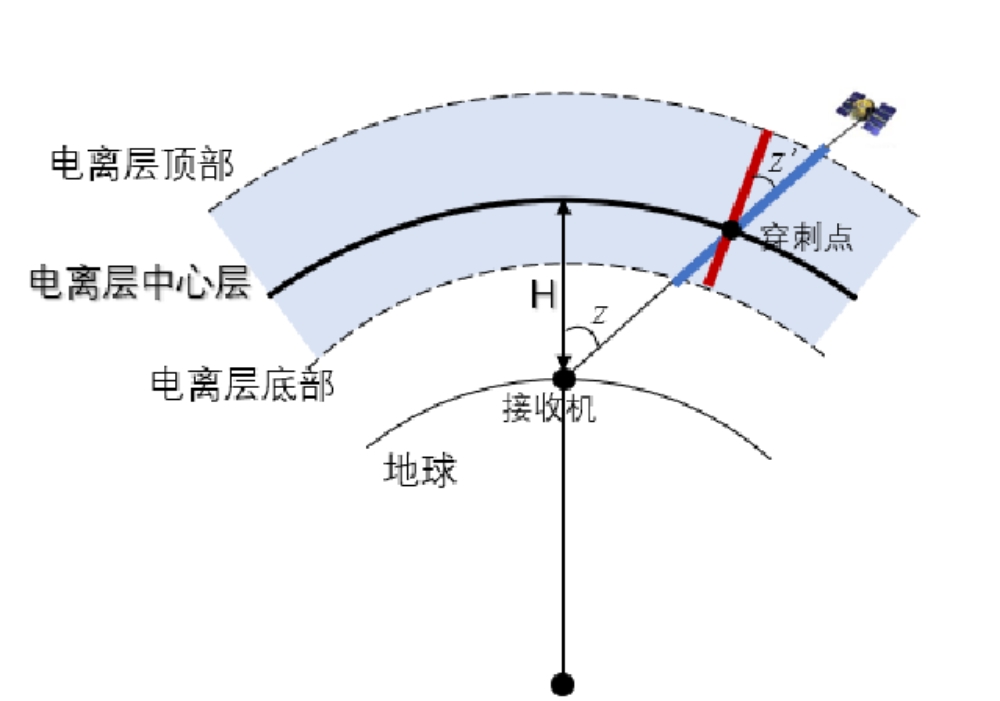
图9.4-4 电离层单层假设图示
上图中,H 为电离层单层高度,一般而言,电离层中心层应当尽可能靠近 F2 层(电子密度最大处)。H 常取的值有 350km、400km、450km 等。
另外,图中蓝色粗线为斜路径电离层延迟 VTEC,其与电离层中心层的交点为穿刺点(Ionospheric Pierce Point,IPP),红色粗线为垂直电离层延迟 VTEC。为实现 STEC 与 VTEC 的灵活转换,由此引入投影函数(Mapping Function,MF)的概念,即 STEC 与 VTEC 的比值。最常用的投影函数是单层模型投影函数 SLM(Single-LayerModel),该模型认为电子密度呈球对称,其表达达式为:
上式中,R 为地球半径,z 和 z' 为上图中的测站相对卫星的天顶距和穿刺点处的天顶距。
2. 参数列表
/* args */
double *pos I receiver position {lat,lon,h} (rad,m)
double *azel I azimuth/elevation angle {az,el} (rad)
/* return */
double res - ionospheric mapping function3. 执行流程
- 高度检查:
- 若接收机高度 (默认 350 公里),返回 1.0(表示无显著投影效应)。
- 映射函数计算:
- 计算 zenith 距离的投影修正:
- 。
- 映射函数 。
- 其中:
- :WGS84 地球参考椭球半径(约 6378137 米)。
- :电离层参考高度(默认 350000 米)。
- :zenith 角。
- 计算 zenith 距离的投影修正:
4. 源码注释
extern double ionmapf(const double *pos, const double *azel)
{
/* 检查接收机高度是否超过电离层参考高度 */
if (pos[2] >= HION) return 1.0; /* 高度 >= HION 时,映射函数为 1 */
/* 计算单层模型映射函数 */
return 1.0 / cos(asin((RE_WGS84 + pos[2]) / (RE_WGS84 + HION) * sin(PI / 2.0 - azel[1])));
/* 公式说明:
* sin(θ) = [(RE_WGS84 + h) / (RE_WGS84 + HION)] * sin(z)
* m = 1 / cos(arcsin(sin(θ)))
* 其中:h = pos[2] (接收机高度), z = π/2 - el (zenith 角) */
}9.4.9 prectrop():精密对流层模型
1. 参数列表
/* args */
gtime_t time I 当前历元时间
double *pos I 基站/移动站位置:纬、经、高
int r I 0 表示移动站,1 表示基站,用来计算对流层状态量在卡尔曼滤波状态矢量的索引
double *azel I 高度角,方位角
prcopt_t *opt I 处理选项
double *x I 卡尔曼滤波状态矢量
double *dtdx IO 对流层湿分量、北向和东向梯度因子
/* return */
double res - 湿延迟值2. 执行流程
- 初始化:
m_w初始化为 0。cotz,grad_n,grad_e用于梯度计算。i = IT(r, opt):获取对流层状态索引(基站或流动站)。
- 湿映射函数计算:
- 调用
tropmapf获取湿分量映射函数 。
- 调用
- 梯度校正(若启用):
- 若 opt->tropopt >= TROPOPT_ESTG 且 azel[1] > 0:
- 计算 cotangent of elevation 角:。
- 计算梯度分量:
- 北向梯度:。
- 东向梯度:。
- 更新 :(加入梯度状态贡献)。
- 计算偏导数:
- (北向梯度对湿延迟的贡献)。
- (东向梯度对湿延迟的贡献)。
- 若 opt->tropopt >= TROPOPT_ESTG 且 azel[1] > 0:
- 无梯度情况:
- 若未启用梯度,设 。
- 输出赋值与返回:
- (湿映射函数赋值)。
- 返回 (湿延迟值)。
3. 源码注释
点击查看代码
/* precise tropospheric model -------------------------------------------------*/
static double prectrop(gtime_t time, const double *pos, int r,
const double *azel, const prcopt_t *opt, const double *x,
double *dtdx)
{
double m_w = 0.0, cotz, grad_n, grad_e; /* 湿映射函数、cot(el)、北向梯度、东向梯度 */
int i = IT(r, opt); /* 获取对流层状态索引 (基站 r=1 或流动站 r=0) */
/* 计算湿映射函数 */
tropmapf(time, pos, azel, &m_w);
/* 梯度校正 (若启用 TROPOPT_ESTG 且高度角 > 0) */
if (opt->tropopt >= TROPOPT_ESTG && azel[1] > 0.0) {
/* 公式:m_w = m_0 + m_0 * cot(el) * (Gn * cos(az) + Ge * sin(az)) [ref 6] */
cotz = 1.0 / tan(azel[1]); /* elevation 角的余切 */
grad_n = m_w * cotz * cos(azel[0]); /* 北向梯度分量 */
grad_e = m_w * cotz * sin(azel[0]); /* 东向梯度分量 */
m_w += grad_n * x[i + 1] + grad_e * x[i + 2]; /* 更新湿映射函数 */
dtdx[1] = grad_n * x[i]; /* 北向梯度偏导数 */
dtdx[2] = grad_e * x[i]; /* 东向梯度偏导数 */
}
else {
dtdx[1] = dtdx[2] = 0.0; /* 未启用梯度时置零 */
}
dtdx[0] = m_w; /* 湿映射函数赋值 */
return m_w * x[i]; /* 返回湿延迟值 */
}9.4.10 constbl():动基线约束
动基线模式:流动站、基准站都在移动,相对距离保持不变,基准站位置由SPP得来,流动站位置由短基线相对定位得到,只有相对位置有意义,绝对位置就是单点定位的精度。
1. 参数列表
/* args */
rtk_t *rtk I rtk 控制/解算结果结构体
const double *x I 状态向量
const double *P I 状态协方差矩阵
double *v O 残差向量
double *H O 雅可比矩阵
double *Ri O 信息矩阵
double *Rj O 信息矩阵
int index I 约束索引
/* return */
int status - 1(成功),0(非线性过大,注释掉的错误返回)2. 执行流程
- 初始化:
- thres = 0.1:非线性阈值(版本 2.3.0 定义)。
- 初始化变量 xb, b, bb, var。
- 基线向量和长度计算:
- xb[i] = rtk->rb[i]:基站位置。
- b[i] = x[i] - xb[i]:基线向量(流动站 - 基站)。
- bb = norm(b, 3):基线长度。
- 方差估算:
- 若 P 有效,计算位置状态的平均方差:
- 。
- 若 P 有效,计算位置状态的平均方差:
- 非线性检查:
- 若 :
- 输出警告(基线长度 bb 和方差 var)。
- 注释掉的返回 0 表示阈值太严格,现继续执行。
- 若 :
- 基线长度约束:
- 残差:(目标长度 - 当前长度)。
- 量测矩阵(若 H 有效):
- (归一化基线向量)。
- 噪声协方差:
- $Ri[index] = 0.0 $(参考噪声)。
- (约束噪声方差)。
3. 源码注释
点击查看代码
/* baseline length constraint ------------------------------------------------*/
static int constbl(rtk_t *rtk, const double *x, const double *P, double *v,
double *H, double *Ri, double *Rj, int index)
{
const double thres = 0.1; /* 非线性阈值 (v.2.3.0) */
double xb[3], b[3], bb, var = 0.0; /* 基站位置、基线向量、基线长度、方差 */
int i;
trace(4, "constbl : \n"); /* 调试:进入函数 */
/* 计算时间调整后的基线向量和长度 */
for (i = 0; i < 3; i++) {
xb[i] = rtk->rb[i]; /* 基站位置 */
b[i] = x[i] - xb[i]; /* 基线向量 (流动站 - 基站) */
}
bb = norm(b, 3); /* 基线长度 */
/* 估算位置状态的平均方差 */
if (P) {
for (i = 0; i < 3; i++) var += P[i + i * rtk->nx];
var /= 3.0;
}
/* 检查非线性 (方差过大时警告) */
if (var > SQR(thres * bb)) {
trace(3, "constbl : pos variance large (bb=%.3f var=%.3f)\n", bb, var);
/* return 0; */ /* 阈值太严格,注释掉但继续执行 */
}
/* 施加基线长度约束 */
v[index] = rtk->opt.baseline[0] - bb; /* 创新 = 目标长度 - 当前长度 */
if (H) {
for (i = 0; i < 3; i++) H[i + index * rtk->nx] = b[i] / bb; /* 量测矩阵 = 归一化基线向量 */
}
Ri[index] = 0.0; /* 参考噪声 */
Rj[index] = SQR(rtk->opt.baseline[1]); /* 约束噪声方差 */
trace(3, "constbl : baseline len v=%13.3f R=%8.6f\n", v[index], Rj[index]); /* 调试:输出创新和噪声 */
return 1; /* 返回成功 */
}9.4.11 ddcov():计算双差量测噪声协方差阵
根据之前计算的单差协方差Ri、Rj 来计算,i==j时为Ri[k+i]+Rj[k+i],i!=j时为Ri[k+i]
1. 参数列表
/* args */
const int *nb I nb[n]: # of sat pairs in group
int n I # of groups (2 for each system, phase and code)
const double *Ri I Ri[nv]: variances of first sats in double diff pairs
const double *Rj I Rj[nv]: variances of 2nd sats in double diff pairs
int nv I total # of sat pairs
double *R O R[nv][nv]: double diff measurement err covariance matrix
/* return */
none2. 执行流程
- 初始化:
- 将 R 矩阵所有元素置 0。
- 输出调试信息(组数 n)。
- 分组循环:
- 外层循环 b 遍历 n 个组,k 跟踪当前组的起始索引(累加 nb[b])。
- 内层循环 i, j 遍历当前组内的卫星对:
- 计算协方差矩阵元素:
- 。
- 若 (对角线),加入第二卫星的方差 ;否则仅为 。
- 计算协方差矩阵元素:
- 调试输出:
- 输出矩阵 (尺寸 )。
3. 源码注释
点击查看代码
/* double-differenced measurement error covariance ---------------------------
* nb[n]: # of sat pairs in group
* n: # of groups (2 for each system, phase and code)
* Ri[nv]: variances of first sats in double diff pairs
* Rj[nv]: variances of 2nd sats in double diff pairs
* nv: total # of sat pairs
* R[nv][nv]: double diff measurement err covariance matrix */
static void ddcov(const int *nb, int n, const double *Ri, const double *Rj,
int nv, double *R)
{
int i, j, k = 0, b;
trace(4, "ddcov : n=%d\n", n); /* 调试:输出组数 */
/* 初始化协方差矩阵为零 */
for (i = 0; i < nv * nv; i++) R[i] = 0.0;
/* 按组循环计算协方差 */
for (b = 0; b < n; k += nb[b++]) { /* 遍历每个系统组 */
for (i = 0; i < nb[b]; i++) {
for (j = 0; j < nb[b]; j++) {
/* 计算双差协方差:Ri + Rj (对角线) 或 Ri (非对角线) */
R[k + i + (k + j) * nv] = Ri[k + i] + (i == j ? Rj[k + i] : 0.0);
}
}
}
trace(5, "R=\n"); tracemat(5, R, nv, nv, 8, 6); /* 调试:输出协方差矩阵 */
}