8.1 estpos():伪距定位
8.1.1 estpos():函数主体
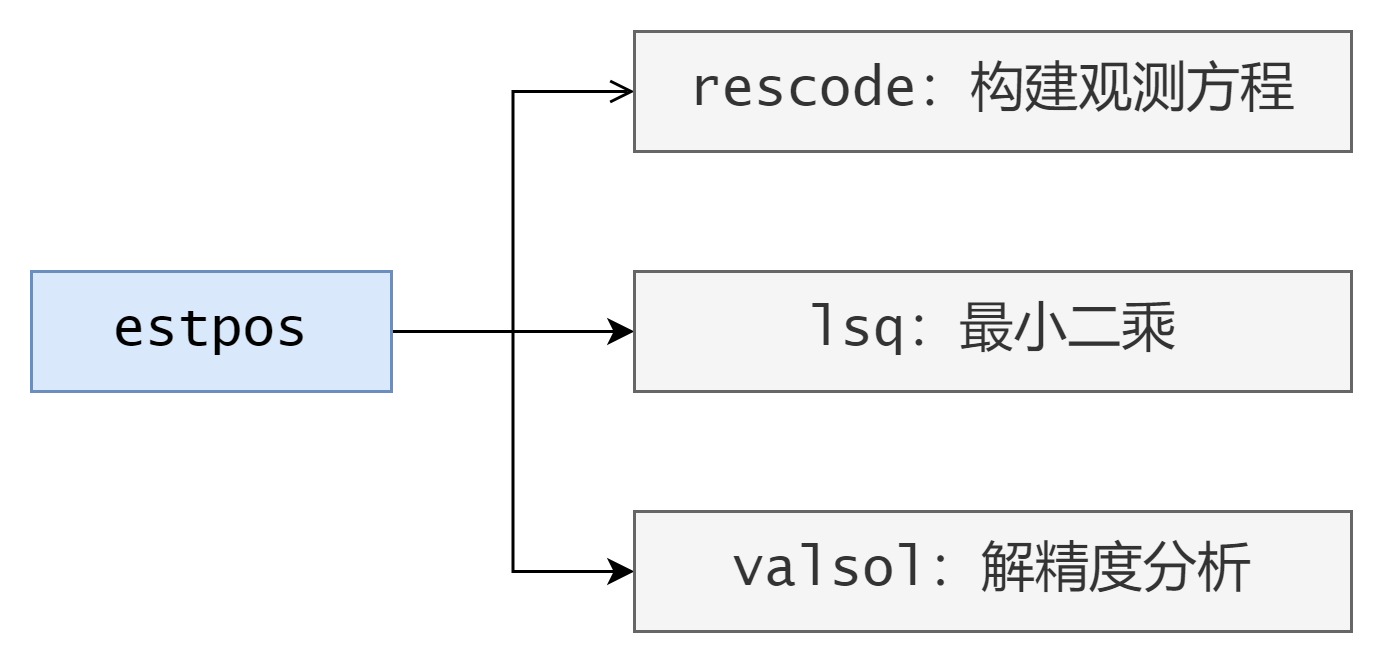
图8.1-1 estpos() 函数调用关系
计算出接收机的位置和钟差,并返回每颗卫星的{方位角、仰角}、定位结果有效性、定位后伪距残差。
1. 参数列表
/* args */
obsd_t *obs I 观测量数据
int n I 观测量数据的数量
double *rs I 卫星位置和速度,长度为6*n,{x,y,z,vx,vy,vz}(ecef)(m,m/s)
double *vare I 卫星位置和钟差的协方差 (m^2)
int *svh I 卫星健康标志 (-1:correction not available)
nav_t *nav I 导航数据
prcopt_t *opt I 处理过程选项
prcopt_t *opt I 处理过程选项
sol_t *sol IO solution
double *azel IO 方位角和俯仰角 (rad)
int *vsat IO 卫星在定位时是否有效
double *resp IO 定位后伪距残差 (P-(r+c*dtr-c*dts+I+T))
char *msg O 错误消息
/* return */
int status - 1:ok,0:error2. 执行流程
- 赋值
x[i]:将sol->rr的前 3 项赋值给x数组(如果是第一次定位,那么x初值为 0)。 - 开始迭代计算(牛顿迭代):迭代次数
MAXITR默认为10。- 调用
rescode():计算当前迭代的伪距残差v、雅可比矩阵H、伪距残差的方差var(用以加权)、所有观测卫星的方位角和仰角azel,定位时有效性vsat、定位后伪距残差resp、参与定位的卫星个数ns和方程个数nv。 - 确定方程组中方程的个数
nv要大于未知数NX的个数。 - 以伪距残差的标准差的倒数
1/sqrt(var)作为权重,对H和v分别左乘权重对角阵,得到加权之后的H和v。 - 调用
lsq()最小二乘函数,得到当前x的改正数dx和定位误差协方差矩阵。 - 将
lsq()中求得的dx加入到当前x值中,得到更新之后的x值 - 如果求得的修改量
dx小于截断因子(目前是1E-4):- 则将
x作为最终的定位结果,对sol的相应参数赋值。 - 之后再调用对定位结果进行卡方检验和 GDOP 检验,检验当前结果是否符合要求(伪距残余小于某个卡方值以及 GDOP 小于某个门限值)。
- 大于截断因子,则进行下一次循环。
- 则将
- 如果超过了规定的循环次数,则输出发散信息后,
return 0。
- 调用
另外提出一个常见的问题:在 GNSS 定位的语境下,雅可比矩阵、几何矩阵和设计矩阵是一回事吗?该问题可以参考 附录 B.6 雅可比矩阵、几何矩阵和设计矩阵。
3. 注意事项
- 关于加权最小二乘:这里的权重值是对角阵,这是建立在假设不同测量值的误差之间是彼此独立的;另外,这个权重值并不单是伪距测量误差的,而是方程右端 b 整体的测量误差。最后,大部分资料上这里都是把权重矩阵 W 保留到方程的解的表达式当中,而这里是直接对 H 和 v 分别左乘权重对角阵,得到加权之后的 H 和 v ,这样做的等价的,其好处是减少运算量。
- 校验函数的使用:如果某次迭代过程中步长小于门限值(1e-4),但经 valsol 函数检验后该解无效,则会直接返回 0,并不会再进行下一次迭代计算。实际上卡方校验的条件过于严格,运用到低成本接收机时可以直接关闭卡方校验。
- sol中的钟差修正:在对 sol 结构体赋值时,sol 中实际存储的是减去接收机钟差后的信号观测时间。
- 估计状态的维度:源码中定位方程的个数 nv 要大于有效观测卫星的个数 ns,这里为了防止亏秩,并且又加了 3 个未知数和观测方程(对应了其他系统的钟差项)。
- rescode的处理:在每一次重新调用 rescode函数时,其内部并没有对 v 、H 和 var 进行清零处理,所以当方程数变少时,可能会存在尾部仍保留上一次数据的情况,但是因为数组相乘时都包含所需计算的长度 nv,所以这种情况并不会对计算结果造成影响。
4. 源码注释
点击查看代码
static int estpos(const obsd_t *obs, int n, const double *rs, const double *dts,
const double *vare, const int *svh, const nav_t *nav,
const prcopt_t *opt, sol_t *sol, double *azel, int *vsat,
double *resp, char *msg)
{
double x[NX]={0},dx[NX],Q[NX*NX],*v,*H,*var,sig;
int i,j,k,info,stat,nv,ns;
trace(3,"estpos : n=%d\n",n);
v=mat(n+4,1); H=mat(NX,n+4); var=mat(n+4,1);
// 赋值x[i]:将 sol->rr 的前 3 项赋值给 x 数组(如果是第一次定位,那么 x 初值为 0)
for (i=0;i<3;i++) x[i]=sol->rr[i];
for (i=0;i<MAXITR;i++) {
// 首先调用 rescode 函数,计算当前迭代的伪距残差 v、雅可比矩阵 H
// 伪距残差的方差 var、所有观测卫星的方位角和仰角 azel、定位时有效性 vsat、
// 定位后伪距残差 resp、参与定位的卫星个数 ns 和方程个数 nv
/* pseudorange residuals (m) */
nv=rescode(i,obs,n,rs,dts,vare,svh,nav,x,opt,v,H,var,azel,vsat,resp,
&ns);
if (nv<NX) { // 确定方程组中方程的个数要大于未知数的个数
sprintf(msg,"lack of valid sats ns=%d",nv);
break;
}
/* weighted by Std */ // 以伪距残差的标准差的倒数作为权重,对 H 和 v 分别左乘权重对角阵,得到加权之后的H和v
for (j=0;j<nv;j++) {
sig=sqrt(var[j]); // 这里的权重值是对角阵,这是建立在假设不同测量值的误差之间是彼此独立的基础上的
// 直接对 H 和 v 分别左乘权重对角阵,得到加权之后的 H 和 v
v[j]/=sig;
for (k=0;k<NX;k++) H[k+j*NX]/=sig;
}
// 调用 lsq 函数,得到当前 x 的修改量 dx 和定位误差协方差矩阵中的权系数阵 Q
/* least square estimation */
if ((info=lsq(H,v,NX,nv,dx,Q))) {
sprintf(msg,"lsq error info=%d",info);
break;
}
// 将lsq中求得的 dx 加入到当前 x 值中,得到更新之后的 x 值
for (j=0;j<NX;j++) {
x[j]+=dx[j];
}
// 如果求得的修改量dx小于截断因子(目前是1E-4),则将x[j]作为最终的定位结果,
// 对 sol 的相应参数赋值,之后再调用 valsol 函数确认当前解是否符合要求,参考 RTKLIB Manual P162
// 否则,进行下一次循环。
if (norm(dx,NX)<1E-4) {
sol->type=0;
// 解方程时的 dtr 单位是 m,是乘以了光速之后的,解出结果后赋给 sol->dtr 时再除以光速
// sol->time 中存储的是减去接收机钟差后的信号观测时间
sol->time=timeadd(obs[0].time,-x[3]/CLIGHT);
sol->dtr[0]=x[3]/CLIGHT; /* receiver clock bias (s) */
sol->dtr[1]=x[4]/CLIGHT; /* GLO-GPS time offset (s) */
sol->dtr[2]=x[5]/CLIGHT; /* GAL-GPS time offset (s) */
sol->dtr[3]=x[6]/CLIGHT; /* BDS-GPS time offset (s) */
sol->dtr[4]=x[7]/CLIGHT; /* IRN-GPS time offset (s) */
for (j=0;j<6;j++) sol->rr[j]=j<3?x[j]:0.0;
for (j=0;j<3;j++) sol->qr[j]=(float)Q[j+j*NX];
sol->qr[3]=(float)Q[1]; /* cov xy */
sol->qr[4]=(float)Q[2+NX]; /* cov yz */
sol->qr[5]=(float)Q[2]; /* cov zx */
sol->ns=(uint8_t)ns;
sol->age=sol->ratio=0.0;
// 对定位结果进行卡方检验和GDOP检验
/* validate solution */
if ((stat=valsol(azel,vsat,n,opt,v,nv,NX,msg))) {
sol->stat=opt->sateph==EPHOPT_SBAS?SOLQ_SBAS:SOLQ_SINGLE;
}
free(v); free(H); free(var);
return stat;
}
}
// 如果超过了规定的循环次数,则输出发散信息后,return 0
if (i>=MAXITR) sprintf(msg,"iteration divergent i=%d",i);
free(v); free(H); free(var);
return 0;
}8.1.2 rescode():残差计算、雅可比矩阵构建
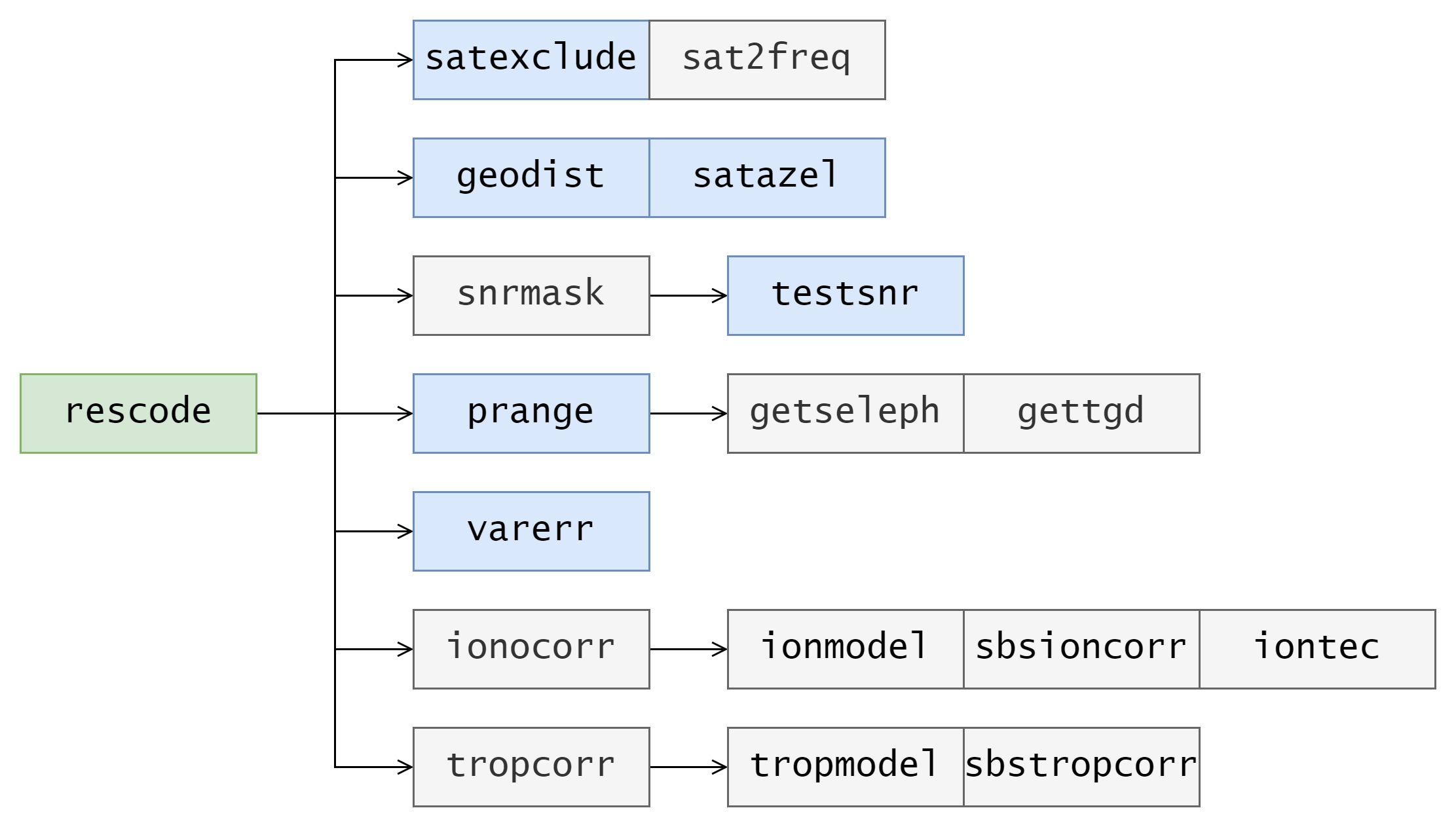
图8.1-2 rescode() 函数调用关系
计算当前迭代的伪距残差 v、雅可比矩阵 H、伪距残差的方差 var、所有观测卫星的方位角和仰角 azel,定位时有效性 vsat、定位后伪距残差 resp、参与定位的卫星个数 ns 和方程个数 nv 。
dion,dtrp,vmeas,vion,vtrp四个局部变量没有初始化, 运行时会报错,可赋初值0.0
1. 参数列表
点击查看代码
/* args */
int iter I 迭代次数,在estpos()里迭代调用,第i次迭代就传i
obsd_t *obs I 观测量数据
int n I 观测量数据的数量
double *rs I 卫星位置和速度,长度为6*n,{x,y,z,vx,vy,vz}(ecef)(m,m/s)
double *dts I 卫星钟差,长度为2*n, {bias,drift} (s|s/s)
double *vare I 卫星位置和钟差的协方差 (m^2)
int *svh I 卫星健康标志 (-1:correction not available)
nav_t *nav I 导航数据
double *x I 本次迭代开始之前的定位值,7*1,前3个是本次迭代开始之前的定位值,第4个是钟差,后三个分别是gps系统与glonass、galileo、bds系统的钟差。
prcopt_t *opt I 处理过程选项
double *v O 定位方程的右端部分,伪距残差
double *H O 定位方程中的雅可比矩阵
double *var O 参与定位的伪距残差的方差
double *azel O 对于当前定位值,所有观测卫星的 {方位角、高度角} (2*n)
int *vsat O 所有观测卫星在当前定位时是否有效 (1*n)
double *resp O 所有观测卫星的伪距残差,(P-(r+c*dtr-c*dts+I+T)) (1*n)
int *ns O 参与定位的卫星的个数
/* return */
int nv - 定位方程组的方程个数2. 执行流程
- 将上一历元的定位信息赋值给
rr和dtr数组。 - 调用
ecef2pos()将将接收机位置rr由 ECEF-XYZ 转换为大地坐标系LLHpos - 遍历当前历元所有
obs[],即遍历每颗卫星:将
vsat[]、azel[]和resp[]数组置 0,因为在前后两次定位结果中,每颗卫星的上述信息都会发生变化。time赋值obs的时间,sat赋值obs的卫星。检测当前观测卫星是否和下一个相邻数据重复;重复则不处理这一条,continue去处理下一条。
调用
satexclude()函数判断卫星是否需要排除,如果排除则continue去处理下一个卫星。调用
geodist()函数,计算卫星和当前接收机位置之间的几何距离r和接收机到卫星的方向向量e。调用
satazel()函数,计算在接收机位置处的站心坐标系中卫星的方位角和仰角;若仰角低于截断值opt->elmin,continue不处理此数据。调用
snrmask(),根据接收机高度角和信号频率来检测该信号是否可用。调用
ionocorr()函数,计算电离层延时I,所得的电离层延时是建立在 L1 信号上的,当使用其它频率信号时,依据所用信号频组中第一个频率的波长与 L1 波长的比率,对上一步得到的电离层延时进行修正。调用
tropcorr()函数,计算对流层延时T。调用
prange()函数,计算经过DCB校正后的伪距值p。计算伪距残差
v[nv],即经过钟差,对流层,电离层改正后的伪距。构建雅可比矩阵
H单点定位的测量方程及其偏导数矩阵构成如下:
公式摘录自 RTKLIB Manual,其中几何距离 和视距(LOS)向量 由 E.3 (3.4) 和 E.3 (3.5) 给出,结合卫星和接收机的位置。卫星位置 和钟差 则根据配置选项“Satellite Ephemeris/Clock”从 E.4 中描述的GNSS卫星星历和时钟推导而来。
处理不同系统(GPS、GLO、GAL、CMP)之间的时间偏差,修改矩阵
H。调用
varerr()函数,计算此时的导航系统误差
- 为了防止不满秩的情况,把矩阵
H补满秩了,H[j+nv*NX]=j==i+3?1.0:0.0;
3. 注意事项
- 返回值
v和resp的主要区别在于长度不一致,v是需要参与定位方程组的解算的,维度为nv*1;而resp仅表示所有观测卫星(包含不健康的卫星)的伪距残余,维度为n*1,对于没有参与定位的卫星,该值为 0,而 nv 小于 n。 - 源码中
dtr的单位是 m。 - 调用
varerr()函数时候,其中的URE值包括:- a. 卫星星历和钟差的误差
- b. 大气延时误差
- c. 伪距测量的码偏移误差
- d. 导航系统的误差
4. 源码注释
点击查看代码
static int rescode(int iter, const obsd_t *obs, int n, const double *rs,
const double *dts, const double *vare, const int *svh,
const nav_t *nav, const double *x, const prcopt_t *opt,
double *v, double *H, double *var, double *azel, int *vsat,
double *resp, int *ns)
{
gtime_t time;
double r, freq, dion = 0.0, dtrp = 0.0, vmeas, vion = 0.0, vtrp = 0.0, rr[3], pos[3], dtr, e[3], P;
int i,j,nv=0,sat,sys,mask[NX-3]={0};
trace(3,"resprng : n=%d\n",n);
// 将之前得到的定位解信息赋值给 rr 和 dtr 数组,以进行关于当前解的伪距残差的相关计算
for (i=0;i<3;i++) rr[i]=x[i];
dtr=x[3];
ecef2pos(rr,pos); // rr{x,y,z}->pos{lat,lon,h}
// 遍历当前历元所有obs[]
for (i=*ns=0;i<n&&i<MAXOBS;i++) {
// 将vsat、azel和resp数组置 0,因为在前后两次定位结果中,每颗卫星的上述信息都会发生变化。
vsat[i]=0; azel[i*2]=azel[1+i*2]=resp[i]=0.0;
time=obs[i].time; // time赋值obs的时间
sat=obs[i].sat; // sat赋值obs的卫星
// 调用satsys()函数,验证卫星编号是否合理及其所属的导航系统
if (!(sys=satsys(sat,NULL))) continue;
// 检测当前观测卫星是否和下一个相邻数据重复;重复则不处理这一条,去处理下一条
/* reject duplicated observation data */
if (i<n-1&&i<MAXOBS-1&&sat==obs[i+1].sat) {
trace(2,"duplicated obs data %s sat=%d\n",time_str(time,3),sat);
i++;
continue;
}
// 处理选项中事先指定定位时排除哪些导航系统或卫星,调用 satexclude 函数完成
/* excluded satellite? */
if (satexclude(sat,vare[i],svh[i],opt)) continue;
// 调用 geodist 函数,计算卫星和当前接收机位置之间的几何距离 r和接收机到卫星方向的观测矢量。
// 然后检验几何距离是否 >0。此函数中会进行地球自转影响的校正(Sagnac效应)
/* geometric distance */
if ((r=geodist(rs+i*6,rr,e))<=0.0) continue;
if (iter>0) {
// 调用 satazel 函数,计算在接收机位置处的站心坐标系中卫星的方位角和仰角;若仰角低于截断值,不处理此数据。
/* test elevation mask */
if (satazel(pos,e,azel+i*2)<opt->elmin) continue;
// 调用snrmask()->testsnr(),根据接收机高度角和信号频率来检测该信号是否可用
/* test SNR mask */
if (!snrmask(obs+i,azel+i*2,opt)) continue;
// 调用 ionocorr 函数,计算电离层延时I,所得的电离层延时是建立在 L1 信号上的,
// 当使用其它频率信号时,依据所用信号频组中第一个频率的波长与 L1 波长的关系,对上一步得到的电离层延时进行修正。
/* ionospheric correction */
if (!ionocorr(time,nav,sat,pos,azel+i*2,opt->ionoopt,&dion,&vion)) {
continue;
}
if ((freq=sat2freq(sat,obs[i].code[0],nav))==0.0) continue;
dion*=SQR(FREQ1/freq);
vion*=SQR(FREQ1/freq);
// 调用 tropcorr 函数,计算对流层延时T
/* tropospheric correction */
if (!tropcorr(time,nav,pos,azel+i*2,opt->tropopt,&dtrp,&vtrp)) {
continue;
}
}
// 调用 prange 函数,得到经过DCB校正后的伪距值 ρ
/* psendorange with code bias correction */
if ((P=prange(obs+i,nav,opt,&vmeas))==0.0) continue;
// 伪距残差 //(P-(r+c*dtr-c*dts+I+T)) (E.6.31)
/* pseudorange residual */
v[nv]=P-(r+dtr-CLIGHT*dts[i*2]+dion+dtrp);
// 构建雅可比矩阵H单位向量的反,前 3 行为中计算得到的视线向,第 4 行为 1,其它行为 0
/* design matrix */
for (j=0;j<NX;j++) {
H[j+nv*NX]=j<3?-e[j]:(j==3?1.0:0.0);
}
// 处理不同系统(GPS、GLO、GAL、CMP)之间的时间偏差,修改矩阵 H
/* time system offset and receiver bias correction */
if (sys==SYS_GLO) {v[nv]-=x[4]; H[4+nv*NX]=1.0; mask[1]=1;}
else if (sys==SYS_GAL) {v[nv]-=x[5]; H[5+nv*NX]=1.0; mask[2]=1;}
else if (sys==SYS_CMP) {v[nv]-=x[6]; H[6+nv*NX]=1.0; mask[3]=1;}
else if (sys==SYS_IRN) {v[nv]-=x[7]; H[7+nv*NX]=1.0; mask[4]=1;}
#if 0 /* enable QZS-GPS time offset estimation */
else if (sys==SYS_QZS) {v[nv]-=x[8]; H[8+nv*NX]=1.0; mask[5]=1;}
#endif
else mask[0]=1;
vsat[i]=1; resp[i]=v[nv]; (*ns)++;
// 调用 varerr 函数,计算此时的导航系统误差,然后累加计算用户测距误差(URE)。
/* variance of pseudorange error */
var[nv++]=varerr(opt,azel[1+i*2],sys)+vare[i]+vmeas+vion+vtrp;
trace(4,"sat=%2d azel=%5.1f %4.1f res=%7.3f sig=%5.3f\n",obs[i].sat,
azel[i*2]*R2D,azel[1+i*2]*R2D,resp[i],sqrt(var[nv-1]));
}
// 防止秩亏:状态中包含不同系统的钟差信息,如果H矩阵不进处理,那么其对应列会出现全0的情况
// 注意:H实际是最小二乘雅可比矩阵的转置
/* constraint to avoid rank-deficient */
for (i=0;i<NX-3;i++) {
if (mask[i]) continue;
v[nv]=0.0;
for (j=0;j<NX;j++) H[j+nv*NX]=j==i+3?1.0:0.0;
var[nv++]=0.01;
}
// 返回值 v和 resp的主要区别在于长度不一致, v是需要参与定位方程组的解算的,维度为 nv*1;
// 而resp仅表示所有观测卫星的伪距残余,维度为 n*1,对于没有参与定位的卫星,该值为 0
return nv;
}8.1.3 lsq(): 最小二乘估计
1. 参数列表
/* args */
double *A I 雅可比矩阵的转置(可含权) (n x m)
double *y I 观测残差项(可含权) (m x 1)
int n,m I 估计参数与观测量的维度 (n<=m)
double *x O 估计参数 (n x 1)
double *Q O 协方差阵 (n x n)
/* return */
int status - 1:ok,0>:error2. 执行过程
- 首先计算右半部分 Ay=A*y 。
- 再计算左半部分括号里面的值 Q=A*A' 。
- 计算 Q 矩阵的逆 Q^-1,但仍存储在 Q 中,最后再右乘 Ay,得到 x 的值。
3. 注意事项
- 关于权重的运算:对于加权最小二乘,可以直接在调用该函数之前直接将 A、y进行加权处理,之后在调用该函数,这样得到的就是加权最小二乘的解。
- RTKLIB的列存储特性:所有的矩阵都是列优先存储的,对于整个源代码来说,矩阵都是这样存储的。所以对于代码中出现的一维矩阵,基本都应该是列向量。在阅读数组下标时,记住这一点是非常重要的。
- 矩阵求逆的特性:矩阵求逆并不简单,尤其是对于接近奇异的矩阵。但是由于这是个基本功能,并不打算继续深入下去。
4. 源码注释
点击查看代码
/* least square estimation -----------------------------------------------------
* least square estimation by solving normal equation (x=(A*A')^-1*A*y)
* args : double *A I transpose of (weighted) design matrix (n x m)
* double *y I (weighted) measurements (m x 1)
* int n,m I number of parameters and measurements (n<=m)
* double *x O estimated parameters (n x 1)
* double *Q O estimated parameters covariance matrix (n x n)
* return : status (0:ok,0>:error)
* notes : for weighted least square, replace A and y by A*w and w*y (w=W^(1/2))
* matrix stored by column-major order (fortran convention)
*-----------------------------------------------------------------------------*/
extern int lsq(const double *A, const double *y, int n, int m, double *x,
double *Q)
{
double *Ay;
int info;
if (m<n) return -1;
Ay=mat(n,1);
matmul("NN",n,1,m,1.0,A,y,0.0,Ay); /* Ay=A*y */
matmul("NT",n,n,m,1.0,A,A,0.0,Q); /* Q=A*A' */
if (!(info=matinv(Q,n))) matmul("NN",n,1,n,1.0,Q,Ay,0.0,x); /* x=Q^-1*Ay */
free(Ay);
return info;
}8.1.4 valsol():对定位结果进行卡方检验和GDOP检验
1. 参数列表
/* args */
const double *azel I 方位角、高度角
const int *vsat I 观测卫星在当前定位时是否有效 (1*n)
int n I 观测值个数
const prcopt_t *opt I 处理选项
const double *v I 定位方程的右端部分,伪距残差
int nv I 观测值数
int nx O 待估计参数数
/* return */
int status - 1:ok,0:error2. 执行流程
其中 是待估参数的数目, 是观测量的数目。 是自由度 和 的卡方分布。GDOP是几何精度因子(dilution of precision)。 可以在“Reject Threshold of GDOP”选项中进行相关配置。
以下为代码的执行流程:
- 先计算定位后伪距残余平方加权和
vv。 - 检查是否满足
vv>chisqr[nv-nx-1],满足条件则说明此时的定位解误差过大,返回 0;否则转到下一步。 - 复制
azel,这里只复制那些对于定位结果有贡献的卫星的zael值,并且统计实现定位时所用卫星的数目。 - 调用
dops函数,计算各种精度因子(DOP),检验是否有0<GDOP<max。否,则说明该定位解的精度不符合要求,返回 0;是,则返回 1。
3. 注意事项
- 低成本接收机可能无法通过卡方校验,可禁用该部分内容(注释掉
return 0); - 代码中的检验与 RTKLIB manual 中不一致(但与教材一致),文档中满足 时就会不合格。与文档中相比,这里的写法将会放宽对于位置解的检验。
8.1.5 satsys():根据卫星编号确定系统与PRN号
RTKLIB 为了方便矩阵的构建与运算,内部对卫星进行了顺序编号(satellite number)。
satsys() 传入卫星satellite number,返回卫星系统和 PRN 号,可以通过笔者编写的转换工具来直观感受这个过程。
1. 参数列表
/* args */
int sat I 卫星编号 (1-MAXSAT)
int *prn IO 卫星 PRN 号或槽号 (NULL则无输出)
/* return */
int sys - 卫星系统 (SYS_GPS,SYS_GLO,...)2. 执行过程
- 为处理意外情况(卫星号不在 1-MAXSAT之内),先令卫星系统为 SYS_NONE。
- 按照 RTKLIB 中定义相应宏的顺序来判断是否是 GPS、GLO、GAL系统等,判断标准是将卫星号减去前面的导航系统所拥有的卫星个数,来判断剩余卫星个数是否小于等于本系统的卫星个数。
- 确定所属的系统后,通过加上最小卫星编号的 PRN再减去 1,得到该卫星在该系统中的 PRN编号。
3. 注意事项
- 这里的卫星号是从 1开始排序的,这也是很多函数中与之有关的数组在调用时形式写为
A[B.sat-1]。
4. 源码注释
点击查看代码
/* satellite number to satellite system ----------------------------------------
* convert satellite number to satellite system
* args : int sat I satellite number (1-MAXSAT)
* int *prn IO satellite prn/slot number (NULL: no output)
* return : satellite system (SYS_GPS,SYS_GLO,...)
*-----------------------------------------------------------------------------*/
extern int satsys(int sat, int *prn)
{
int sys=SYS_NONE;
if (sat<=0||MAXSAT<sat) sat=0;
else if (sat<=NSATGPS) {
sys=SYS_GPS; sat+=MINPRNGPS-1;
}
else if ((sat-=NSATGPS)<=NSATGLO) {
sys=SYS_GLO; sat+=MINPRNGLO-1;
}
else if ((sat-=NSATGLO)<=NSATGAL) {
sys=SYS_GAL; sat+=MINPRNGAL-1;
}
else if ((sat-=NSATGAL)<=NSATQZS) {
sys=SYS_QZS; sat+=MINPRNQZS-1;
}
else if ((sat-=NSATQZS)<=NSATCMP) {
sys=SYS_CMP; sat+=MINPRNCMP-1;
}
else if ((sat-=NSATCMP)<=NSATIRN) {
sys=SYS_IRN; sat+=MINPRNIRN-1;
}
else if ((sat-=NSATIRN)<=NSATLEO) {
sys=SYS_LEO; sat+=MINPRNLEO-1;
}
else if ((sat-=NSATLEO)<=NSATSBS) {
sys=SYS_SBS; sat+=MINPRNSBS-1;
}
else sat=0;
if (prn) *prn=sat;
return sys;
}8.1.6 satexclude():检测是否排除某颗卫星
1. 参数列表
函数参数,3个
int sat I 卫星编号,从 1开始
int svh I sv 健康标识 (0:ok)
prcopt_t *opt I 配置参数 (NULL: not used)
返回类型:
int status - 1:排除, 0:不排除2. 执行过程
- 首先调用
satsys函数得到该卫星所属的导航系统。 - 接着检验
svh<0。是,则说明在ephpos函数中调用seleph为该卫星选择星历时,并无合适的星历可用,返回 1;否,则进入下一步。 - 如果处理选项不为空,则检测处理选项中对该卫星的排除标志的值(1:excluded,2:included),之后再检测该卫星所属的导航系统与处理选项中预先设定的是否一致。否,返回 1;是,进入下一步。
- 如果此时
svh>0,说明此时卫星健康状况出现问题,此卫星不可用,返回 1。
3. 问题思考
- satexclude的作用机制:对于步骤3中检测,先验证状态排除标志,后验证导航系统,这样就可能出现排除标志符合要求而所属系统不符合要求的状况,而步骤3中做法会将上述状况设为 included。又或者,在步骤3中检测之后仍验证了
svh>0,那如果出现svh不合乎要求而排除标志符合要求的状况,步骤3中做法却会将上述状况设为 included。该部分内容可以参考附录B.3。
4. 源码注释
点击查看代码
extern int satexclude(int sat, double var, int svh, const prcopt_t *opt)
{
int sys=satsys(sat,NULL);
// 通过svh判断卫星是否健康可用
/* ephemeris unavailable */
if (svh<0) return 1;
if (opt) {
if (opt->exsats[sat-1]==1) return 1; /* excluded satellite */
if (opt->exsats[sat-1]==2) return 0; /* included satellite */
if (!(sys&opt->navsys)) return 1; /* unselected sat sys */ // 比较该卫星与预先规定的导航系统是否一致
}
if (sys==SYS_QZS) svh&=0xFE; /* mask QZSS LEX health */
if (svh) {
trace(3,"unhealthy satellite: sat=%3d svh=%02X\n",sat,svh);
return 1;
}
if (var>MAX_VAR_EPH) {
trace(3,"invalid ura satellite: sat=%3d ura=%.2f\n",sat,sqrt(var));
return 1;
}
return 0;
}8.1.7 testsnr():检测信号是否可用
testsnr() 在 snrmask() 内部调用。
1. 参数列表
/* args */
int base I rover or base-station (0:rover,1:base station)
int freq I frequency (0:L1,1:L2,2:L3,...)
double el I elevation angle (rad)
double snr I C/N0 (dBHz)
snrmask_t *mask I SNR mask
/* return */
int status - 1:masked,0:unmasked2. 执行流程
- 满足下列情况之一
!mask->ena[base]||freq<0||freq>=NFREQ,返回 0. - 对
el处理变换,根据后面i的值得到不同的阈值minsnr,而对1<=i<=8的情况,则使用线性插值计算出minsnr的值。
3. 源码注释
点击查看代码
extern int testsnr(int base, int idx, double el, double snr,
const snrmask_t *mask)
{
double minsnr,a;
int i;
if (!mask->ena[base]||idx<0||idx>=NFREQ) return 0;
a=(el*R2D+5.0)/10.0;
i=(int)floor(a); a-=i;
if (i<1) {
minsnr=mask->mask[idx][0];
}
else if (i>8) {
minsnr=mask->mask[idx][8];
}
else {
// 1<=i<=8 的情况,则使用线性插值计算出 minsnr 的值
minsnr=(1.0-a)*mask->mask[idx][i-1]+a*mask->mask[idx][i];
}
return snr<minsnr; // snr 小于 minsnr 时,返回1
}8.1.8 geodist():计算站心几何距离
1. 基本原理
地球自转引起的误差源自于信号传输过程中:GNSS 卫星信号发射时刻和接收机接收到信号的时刻之间地球自转对 GNSS 观测值产生的影响。
相当于地球自转使得卫星空间位置在信号播发、接收过程中接收机在地固系坐标轴上相对于 z 轴发生了一定角度的旋转,使得 GNSS 卫星的在信号发射时刻的位置发生了变化,该现象也称作 Sagnac 效应。
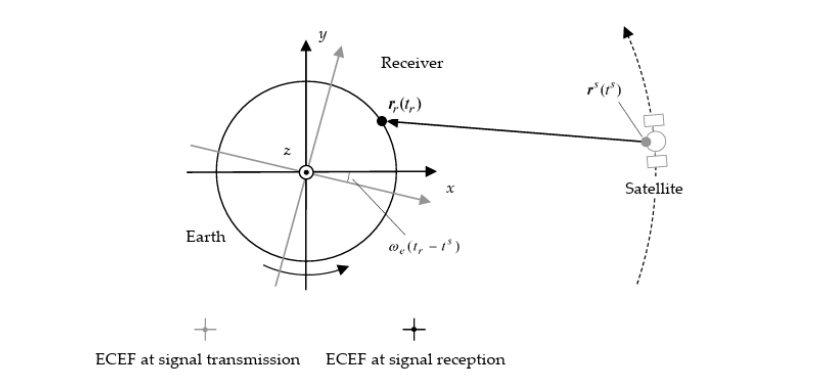
图10-2 几何距离和地球自转校正
地球自转引起的距离改正公式如下:
上式中 为地球自旋转后卫星的坐标值, 为地球自旋转前卫星的坐标值, 代表地球自传角速度值, 为卫星发射信号时刻到接收机接收卫星时刻的历元数。改正地球自转后的近似几何距离近似几何距离如下:
接收机到卫星方向的观测矢量计算公式如下:
2. 参数列表
/* args */
double *rs I satellite position (ecef at transmission) (m)
double *rr I receiver position (ecef at reception) (m)
double *e O line-of-sight unit vector (ecef)
/* return */
double dis - geometric distance (m) (0>:error/no satellite position)3. 执行流程
- 检查卫星到 WGS84 坐标系原点的距离是否大于基准椭球体的长半径。
ps-pr,计算由接收机指向卫星方向的观测矢量,之后在计算出相应的单位矢量。- 考虑到地球自转,即信号发射时刻卫星的位置与信号接收时刻卫星的位置在 WGS84 坐标系中并不一致,进行关于 Sagnac 效应的校正。
4. 源码注释
点击查看代码
extern double geodist(const double *rs, const double *rr, double *e)
{
double r;
int i;
if (norm(rs,3)<RE_WGS84) return -1.0; // 检查卫星到 WGS84坐标系原点的距离是否大于基准椭球体的长半径。
for (i=0;i<3;i++) e[i]=rs[i]-rr[i]; // 求卫星和接收机坐标差e[]
r=norm(e,3); // 求未经萨格纳克效应改正的距离
for (i=0;i<3;i++) e[i]/=r; // 接收机到卫星的单位向量e[] (E.3.9)
return r+OMGE*(rs[0]*rr[1]-rs[1]*rr[0])/CLIGHT; // (E.3.8b)
}8.1.9 satazel():计算方位角、高度角
1. 基本原理
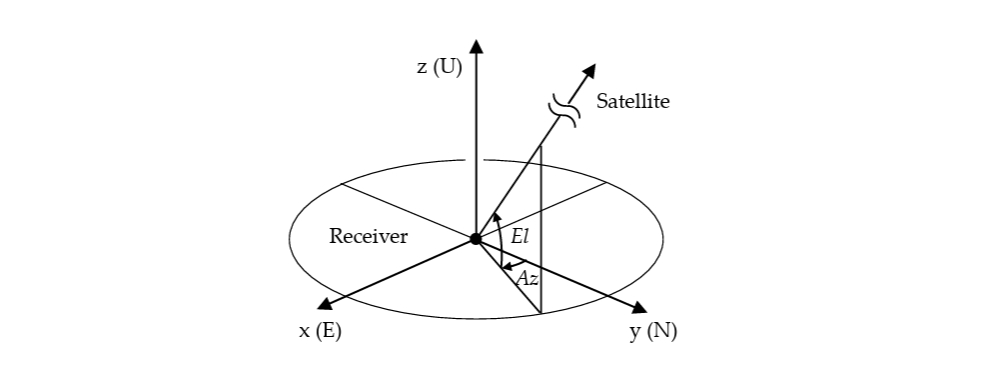
图10-3 局部坐标系与方位角和仰角
方位角范围在 ,高度角范围在 ;以接收机为原点,建立站心坐标系 ENU,根据卫星 ENU 下方向矢量可以得到高度角、方位角,公式如下:
对应的代码如下,传入接收机 LLH 坐标 pos、接收机到卫星方向的观测矢量 e,计算之后返回弧度制的高度角,如果传了参三 azel,那么 azel[0] 是方位角、azel[1] 是高度角。
2. 参数列表
/* args */
double *pos I geodetic position {lat,lon,h} (rad,)
double *e I receiver-to-satellilte unit vevtor (ecef)
double *azel IO azimuth/elevation {az,el} (rad) (NULL: no output) (0.0<=azel[0]<2*pi,-pi/2<=azel[1]<=pi/2)
/* return */
double angle - elevation angle (rad)3. 执行流程
- 调用
ecef2enu函数,将pos处的向量转换到以改点为原点的站心坐标系中。 - 调用
atan2函数计算出方位角,然后再算出仰角。
4. 注意事项
- 这里在计算方位角时,要使用
atan2函数,而不能是atan函数,详细原因见附录A.5。
5. 源码注释
点击查看代码
extern double satazel(const double *pos, const double *e, double *azel)
{
double az=0.0,el=PI/2.0,enu[3];
if (pos[2]>-RE_WGS84) {
ecef2enu(pos,e,enu);
az=dot(enu,enu,2)<1E-12?0.0:atan2(enu[0],enu[1]);
if (az<0.0) az+=2*PI;
el=asin(enu[2]);
}
if (azel) {azel[0]=az; azel[1]=el;}
return el;
}8.1.10 prange():计算经过DCB校正后的伪距值p
差分码偏差(DCB)是 GNSS 伪距观测中由不同测距码信号(如 C1、P1、P2)在卫星和接收机硬件通道中产生的时延差异。分为:
- 频内偏差:同一频率不同码的时延差,如 P1-C1。
- 频间偏差:不同频率码的时延差,如 P1-P2。
DCB 由信号生成至发射的硬件时延差异引起,校正 DCB 可提高 GNSS 定位精度。
1. 参数列表
/* args */
obsd_t *obs I 观测数据
nav_t *nav I 导航数据
double *azel I 对于当前定位值,每一颗观测卫星的 {方位角、高度角}
int iter I 迭代次数
prcopt_t *opt I 配置参数
double *vare O 伪距测量的码偏移误差
/* return */
double P1 - 最终参与定位解算的伪距值2. 执行流程
点击查看更多
- 初始化和基本检查
- 获取卫星编号和系统类型(如 GPS、GLONASS)。
- 获取 L1/E1/B1 伪距(P1)和第二频率伪距(P2,由 seliflc 选择,如 L2、L5)。
- 初始化方差 *var = 0.0。
- 检查观测值有效性:若 P1 为 0 或 IFLC 模式下 P2 为 0,返回 0.0(无效观测)。
- DCB 校正
- L1/E1/B1 校正:通过 code2bias_ix 获取 L1 频率测距码的 DCB 索引(bias_ix),若非参考码(bias_ix > 0),校正 P1。
- L2/L5 校正:对第二频率伪距(P2)进行类似校正,但 Galileo 的 L2(f2 == 1)无 DCB 数据,跳过校正。
- DCB 数据存储在 nav->cbias,按系统、频率和码类型索引。
- 双频无电离层组合(IFLC)
- GPS/QZSS(L1-L2 或 L1-L5)c
// 使用 L1/L2(FREQL1/FREQL2)或 L1/L5(FREQL1/FREQL5)频率比的平方 gamma = f2 == 1 ? SQR(FREQL1/FREQL2) : SQR(FREQL1/FREQL5); return (P2 - gamma * P1) / (1.0 - gamma); - GLONASS(G1-G2 或 G1-G3)c
// 使用 GLONASS 频率(如 G1/G2 或 G1/G3) gamma = f2 == 1 ? SQR(FREQ1_GLO/FREQ2_GLO) : SQR(FREQ1_GLO/FREQ3_GLO); return (P2 - gamma * P1) / (1.0 - gamma); - Galileo(E1-E5b 或 E1-E5a)c
// 使用 E1/E5b 或 E1/E5a 频率比。 // 对 F/NAV 星历(getseleph(SYS_GAL)),校正 E5a/E5b 的广播群延迟(BGD)。 gamma = f2 == 1 ? SQR(FREQL1/FREQE5b) : SQR(FREQL1/FREQL5); if (f2 == 1 && getseleph(SYS_GAL)) { P2 -= gettgd(sat, nav, 0) - gettgd(sat, nav, 1); /* BGD_E5aE5b */ } return (P2 - gamma * P1) / (1.0 - gamma); - BeiDou(B1-B2)c
// 支持 B1I/B1Cp/B1Cd 码,校正 TGD(b1, b2) // 公式包含 TGD 校正:$P_{IF} = \frac{(P_2 - b_2) - \gamma (P_1 - b_1)}{1 - \gamma}$ gamma = SQR(((obs->code[0] == CODE_L2I) ? FREQ1_CMP : FREQL1) / FREQ2_CMP); if (obs->code[0] == CODE_L2I) b1 = gettgd(sat, nav, 0); /* TGD_B1I */ else if (obs->code[0] == CODE_L1P) b1 = gettgd(sat, nav, 2); /* TGD_B1Cp */ else b1 = gettgd(sat, nav, 2) + gettgd(sat, nav, 4); /* TGD_B1Cp+ISC_B1Cd */ b2 = gettgd(sat, nav, 1); /* TGD_B2I/B2bI (m) */ return ((P2 - gamma * P1) - (b2 - gamma * b1)) / (1.0 - gamma); - IRNSS(L5-S)
- GPS/QZSS(L1-L2 或 L1-L5)
- 单频伪距校正 当非 IFLC 模式(单频),直接使用 L1/E1/B1 伪距,并校正 TGD:
- GPS/QZSS:校正 L1 的 TGD(b1)。
- GLONASS:校正 G1 的 TGD,考虑频率比 。
- Galileo:校正 E1 的 BGD(E1-E5a 或 E1-E5b)。
- BeiDou:根据码类型(B1I/B1Cp/B1Cd)校正 TGD。
- IRNSS:校正 L5 的 TGD,考虑频率比。
- 方差设为 SQR(ERR_CBIAS),表示单频伪距的码偏差误差。
3. 注意事项
- prange 的直接作用: 主要是是计算 GNSS 伪距观测值,经过差分码偏差(DCB)校正、广播群延迟(TGD/BGD)校正,并根据用户选项(
opt->ionoopt)选择 无电离层线性组合(IFLC) 或 单频伪距 的处理方式。该函数并不直接针对 C/A 码(如 C1)进行特定修正,而是对所有测距码(如 C1、P1、P2 等)应用通用的 DCB 和 TGD 校正,以消除硬件时延和电离层效应。
点击查看代码
/* 计算伪距(无电离层组合或单频),包含DCB和TGD/BGD校正 */
static double prange(const obsd_t *obs, const nav_t *nav, const prcopt_t *opt,
double *var)
{
double P1, P2, gamma, b1, b2; /* P1, P2: 伪距; gamma: 频率比平方; b1, b2: TGD/BGD */
int sat, sys, f2, bias_ix; /* sat: 卫星编号; sys: 系统类型; f2: 第二频率索引; bias_ix: DCB索引 */
/* 初始化变量 */
sat = obs->sat; /* 获取卫星编号 */
sys = satsys(sat, NULL); /* 获取卫星系统(如GPS、GLONASS) */
P1 = obs->P[0]; /* 获取L1/E1/B1伪距 */
f2 = seliflc(opt->nf, satsys(obs->sat, NULL)); /* 选择第二频率(如L2、L5) */
P2 = obs->P[f2]; /* 获取L2/L5/E5等伪距 */
*var = 0.0; /* 初始化方差 */
/* 检查观测值有效性:P1为0或IFLC模式下P2为0,返回0.0 */
if (P1 == 0.0 || (opt->ionoopt == IONOOPT_IFLC && P2 == 0.0)) return 0.0;
/* 校正L1/E1/B1的DCB(频内偏差,如P1-C1) */
bias_ix = code2bias_ix(sys, obs->code[0]); /* 获取L1测距码的DCB索引 */
if (bias_ix > 0) { /* 非参考码(bias_ix=0为参考码) */
P1 += nav->cbias[sat-1][0][bias_ix-1]; /* 应用L1 DCB校正 */
}
/* 校正L2/L5/E5的DCB(频内偏差,如P2-C2) */
if (sys == SYS_GAL && f2 == 1) {
/* Galileo L2无DCB数据,跳过校正 */
} else {
bias_ix = code2bias_ix(sys, obs->code[f2]); /* 获取第二频率测距码的DCB索引 */
if (bias_ix > 0) { /* 非参考码 */
P2 += nav->cbias[sat-1][1][bias_ix-1]; /* 应用L2/L5 DCB校正 */
}
}
/* 双频无电离层组合(IFLC)处理 */
if (opt->ionoopt == IONOOPT_IFLC) {
if (sys == SYS_GPS || sys == SYS_QZS) { /* GPS/QZSS: L1-L2或L1-L5 */
gamma = f2 == 1 ? SQR(FREQL1/FREQL2) : SQR(FREQL1/FREQL5); /* 计算频率比平方 */
*var = SQR(3.0) * SQR(ERR_CBIAS); /* 近似方差放大(噪声放大因子≈3.0) */
return (P2 - gamma * P1) / (1.0 - gamma); /* IFLC公式 */
} else if (sys == SYS_GLO) { /* GLONASS: G1-G2或G1-G3 */
gamma = f2 == 1 ? SQR(FREQ1_GLO/FREQ2_GLO) : SQR(FREQ1_GLO/FREQ3_GLO);
*var = SQR(3.0) * SQR(ERR_CBIAS); /* 近似方差放大 */
return (P2 - gamma * P1) / (1.0 - gamma);
} else if (sys == SYS_GAL) { /* Galileo: E1-E5b或E1-E5a */
gamma = f2 == 1 ? SQR(FREQL1/FREQE5b) : SQR(FREQL1/FREQL5);
if (f2 == 1 && getseleph(SYS_GAL)) { /* F/NAV星历,校正BGD */
P2 -= gettgd(sat, nav, 0) - gettgd(sat, nav, 1); /* BGD_E5aE5b */
}
*var = SQR(3.0) * SQR(ERR_CBIAS); /* 近似方差放大 */
return (P2 - gamma * P1) / (1.0 - gamma);
} else if (sys == SYS_CMP) { /* BeiDou: B1-B2 */
gamma = SQR(((obs->code[0] == CODE_L2I) ? FREQ1_CMP : FREQL1) / FREQ2_CMP);
if (obs->code[0] == CODE_L2I) b1 = gettgd(sat, nav, 0); /* TGD_B1I */
else if (obs->code[0] == CODE_L1P) b1 = gettgd(sat, nav, 2); /* TGD_B1Cp */
else b1 = gettgd(sat, nav, 2) + gettgd(sat, nav, 4); /* TGD_B1Cp+ISC_B1Cd */
b2 = gettgd(sat, nav, 1); /* TGD_B2I/B2bI */
*var = SQR(3.0) * SQR(ERR_CBIAS); /* 近似方差放大 */
return ((P2 - gamma * P1) - (b2 - gamma * b1)) / (1.0 - gamma); /* IFLC含TGD校正 */
} else if (sys == SYS_IRN) { /* IRNSS: L5-S */
gamma = SQR(FREQL5/FREQs);
*var = SQR(3.0) * SQR(ERR_CBIAS); /* 近似方差放大 */
return (P2 - gamma * P1) / (1.0 - gamma);
}
} else { /* 单频(L1/E1/B1)处理 */
*var = SQR(ERR_CBIAS); /* 单频方差,基于码偏差误差 */
if (sys == SYS_GPS || sys == SYS_QZS) { /* GPS/QZSS: L1 */
b1 = gettgd(sat, nav, 0); /* TGD */
return P1 - b1;
} else if (sys == SYS_GLO) { /* GLONASS: G1 */
gamma = SQR(FREQ1_GLO/FREQ2_GLO);
b1 = gettgd(sat, nav, 0); /* -dtaun */
return P1 - b1 / (gamma - 1.0);
} else if (sys == SYS_GAL) { /* Galileo: E1 */
if (getseleph(SYS_GAL)) b1 = gettgd(sat, nav, 0); /* BGD_E1E5a */
else b1 = gettgd(sat, nav, 1); /* BGD_E1E5b */
return P1 - b1;
} else if (sys == SYS_CMP) { /* BeiDou: B1I/B1Cp/B1Cd */
if (obs->code[0] == CODE_L2I) b1 = gettgd(sat, nav, 0); /* TGD_B1I */
else if (obs->code[0] == CODE_L1P) b1 = gettgd(sat, nav, 2); /* TGD_B1Cp */
else b1 = gettgd(sat, nav, 2) + gettgd(sat, nav, 4); /* TGD_B1Cp+ISC_B1Cd */
return P1 - b1;
} else if (sys == SYS_IRN) { /* IRNSS: L5 */
gamma = SQR(FREQs/FREQL5);
b1 = gettgd(sat, nav, 0); /* TGD */
return P1 - gamma * b1;
}
}
return P1; /* 默认返回L1伪距 */
}8.1.11 varerr():计算导航系统伪距测量值的误差
varerr()一定程度上代表了误差的水平,该函数是衡量载波相位误差的函数,通过fact因子(如300)可以放缩到伪距误差的水平。有关观测误差模型的更多内容,可以参考附录C.3。
1. 参数列表
/* args */
prcopt_t *opt I processing options
double el I elevation angle (rad)
int sys I 所属的导航系统
/* return */
double varr - 导航系统伪距测量值的误差2. 执行流程
- 确定 sys系统的误差因子。
- 计算由导航系统本身所带来的误差的方差。
- 如果 ionoopt==IONOOPT_IFLC时,IFLC模型的方差也会添加到最终计算得到的方差中。
3. 问题思考
- IFLC 模型的方差为什么使用
varr*=SQR(3.0)计算?该部分参考附录B.4。
4. 源码注释
点击查看代码
/* 这里的代码使用的是demo5版本 */
static double varerr(const prcopt_t *opt, const ssat_t *ssat, const obsd_t *obs, double el, int sys)
{
double fact=1.0,varr,snr_rover;
switch (sys) {
case SYS_GPS: fact *= EFACT_GPS; break; // fact=1.0
case SYS_GLO: fact *= EFACT_GLO; break; // fact=1.5
case SYS_SBS: fact *= EFACT_SBS; break; // fact=3.0
case SYS_CMP: fact *= EFACT_CMP; break; // fact=1.0
case SYS_QZS: fact *= EFACT_QZS; break; // fact=1.0
case SYS_IRN: fact *= EFACT_IRN; break; // fact=1.5
default: fact *= EFACT_GPS; break; // fact=1.0
}
// 高度角过小,设为5°
if (el<MIN_EL) el=MIN_EL;
/* var = R^2*(a^2 + (b^2/sin(el) + c^2*(10^(0.1*(snr_max-snr_rover)))) + (d*rcv_std)^2) */
varr=SQR(opt->err[1])+SQR(opt->err[2])/sin(el);
if (opt->err[6]>0.0) { /* if snr term not zero */
snr_rover=(ssat)?SNR_UNIT*ssat->snr_rover[0]:opt->err[5];
varr+=SQR(opt->err[6])*pow(10,0.1*MAX(opt->err[5]-snr_rover,0));
}
varr*=SQR(opt->eratio[0]);
if (opt->err[7]>0.0) {
varr+=SQR(opt->err[7]*0.01*(1<<(obs->Pstd[0]+5))); /* 0.01*2^(n+5) m */
}
/* iono-free */ // 无电离层组合,方差*3*3
if (opt->ionoopt==IONOOPT_IFLC) varr*=SQR(3.0);
return SQR(fact)*varr;
}