11. RTKLIB工程优化

11.1 数据处理

11.1.1 北斗频点调整

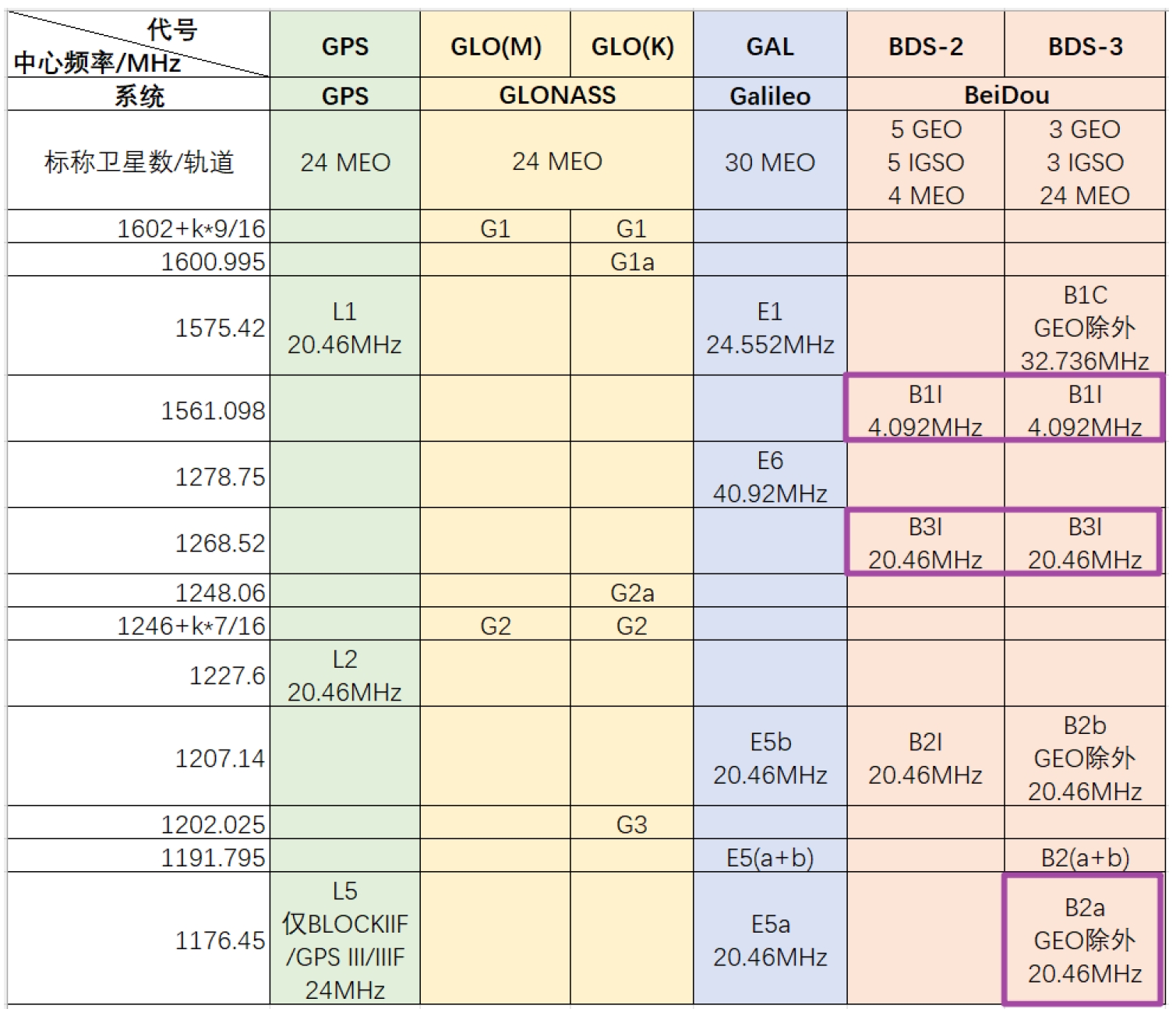
现在将B1I/B3I/B2a作为北斗的三个频点，而不考虑北斗3的B1C信号与北斗2的B2I信号。该调整能更方便地使用北斗3代的B2a信号（作为L5信号），该组合在双频L1/L5的情况下表现更好，另外该调整在RTKLIB Demo5的b34k版本中也得到了更新，对应实现的代码参考附录A.1。

另外RTK的滤波算法中没有使用QZSS和GLO，没使用QZSS是因为卫星太少，而GLO则是因为国内没有差分数据。

11.2 单点定位

由于最小二乘较为简单，能比较方便和快速地对一些方法进行验证，因此初始时我将利用最小二乘进行一些基础的优化。这部分的优化可以参考项目：MobileGNSS-SPP

11.2.1 加权模型

1. RTKLIB中的BUG

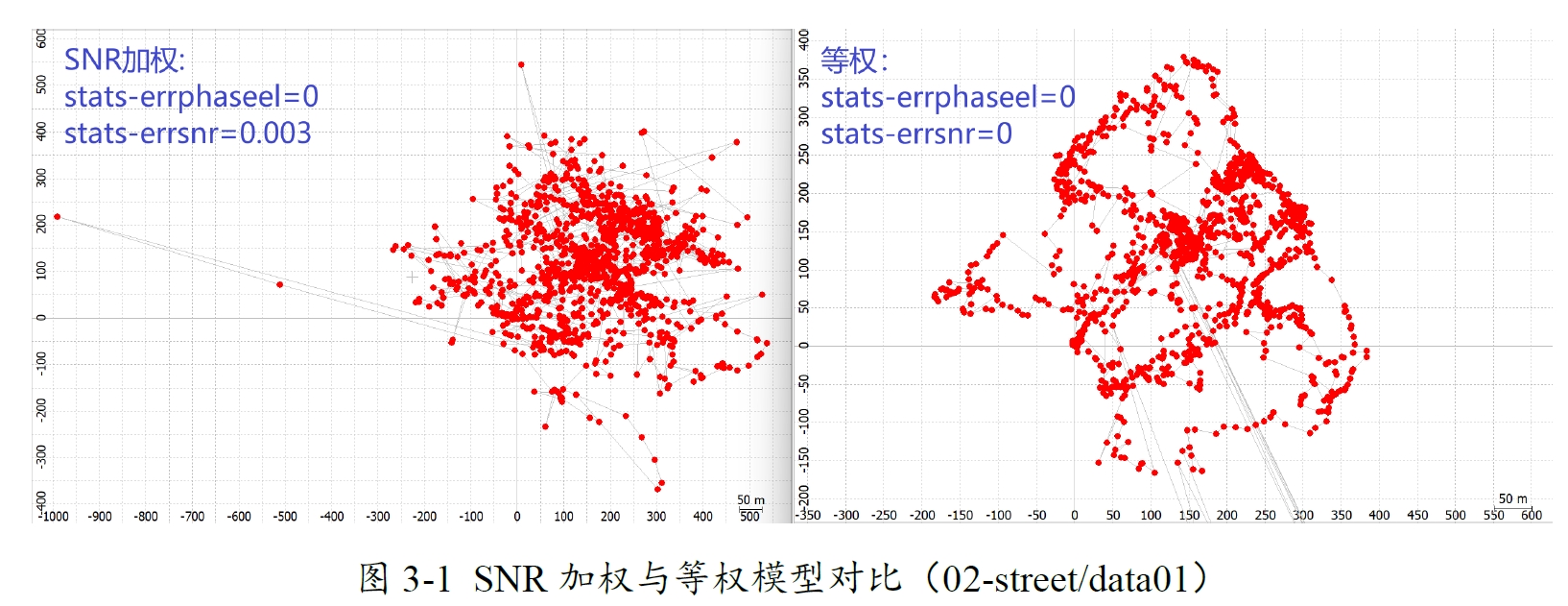
demo5-b34k版本的RTKLIB在打开SNR加权后轨迹会崩溃，不过这并不是因为SNR加权效果不如等权，这里显然是错误，而非误差。

将ssat[i]改成ssat[sat-1]即可解决，打开SNR加权将提升定位性能。

2. 仰角与SNR加权

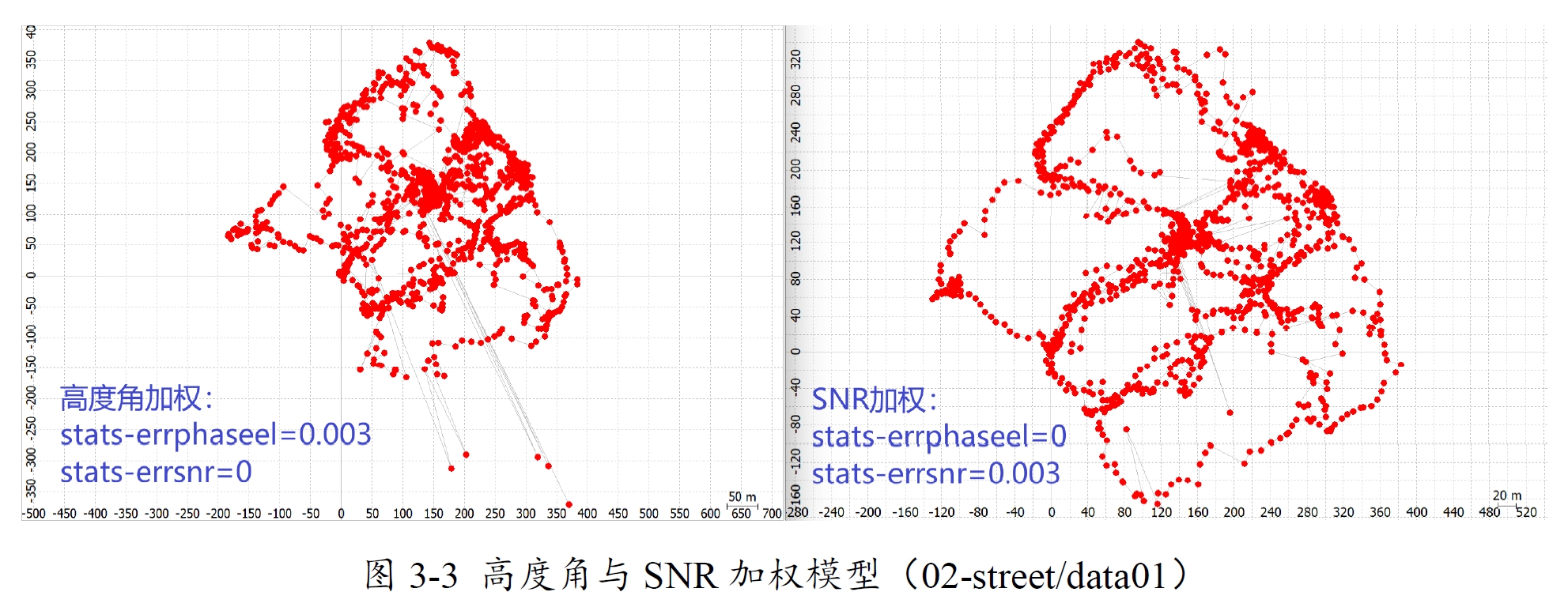
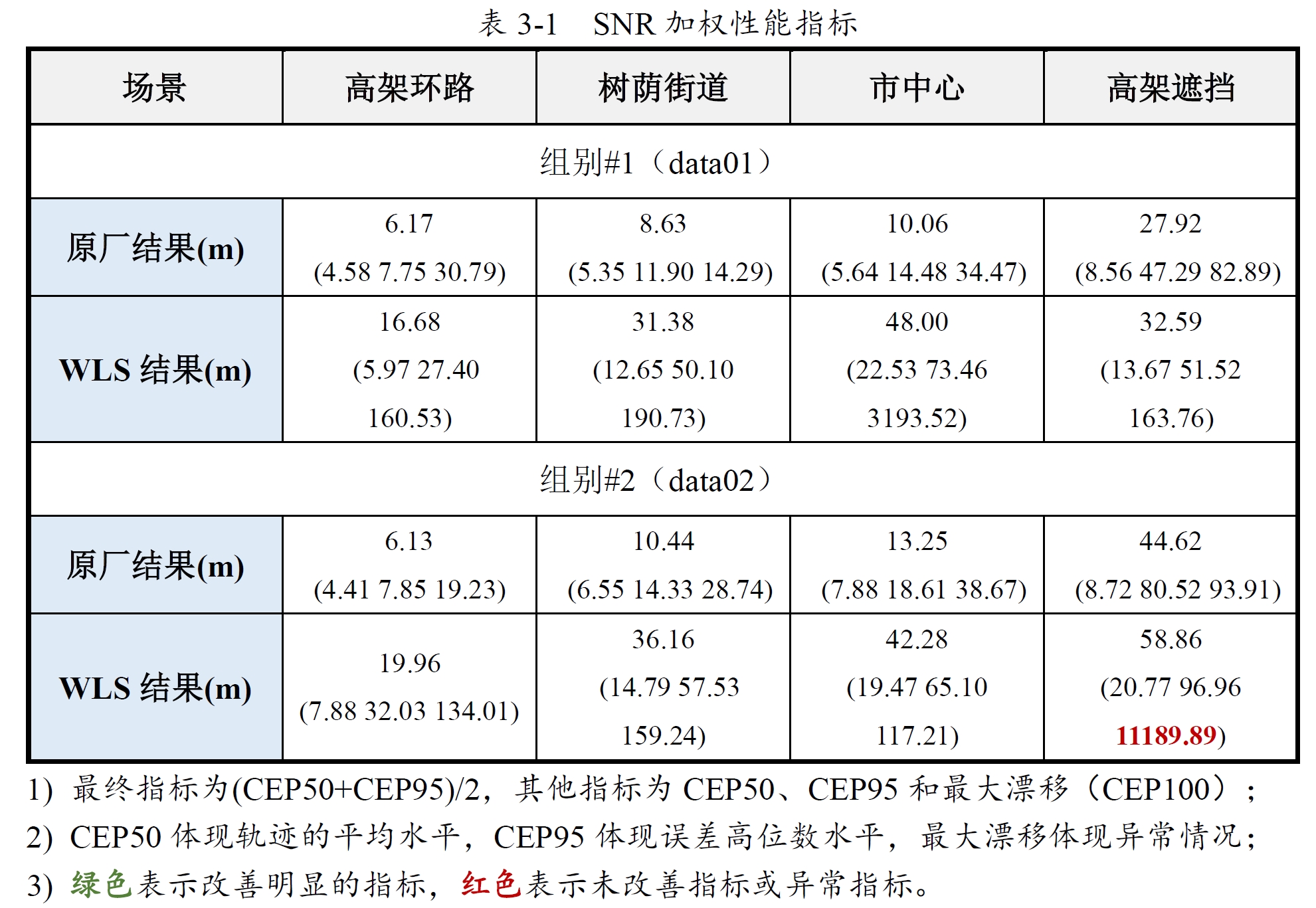
以上为使用SNR加权模型WLS在不同场景上的表现，目前由于代码中没有抗差，因此最大漂移指标都比较大。

基于卫星仰角的GNSS观测模型更适用于专用接收机。然而，对于智能手机，基于信号强度（载噪比，C/N0）的模型比依赖仰角的模型更能有效地处理观测权重[4,5,6]。因为智能手机观测误差往往由信号质量问题主导，而非大气误差，而使用仰角加权观测的动机正是为了解决大气误差

11.2.2 速度估计中的加权

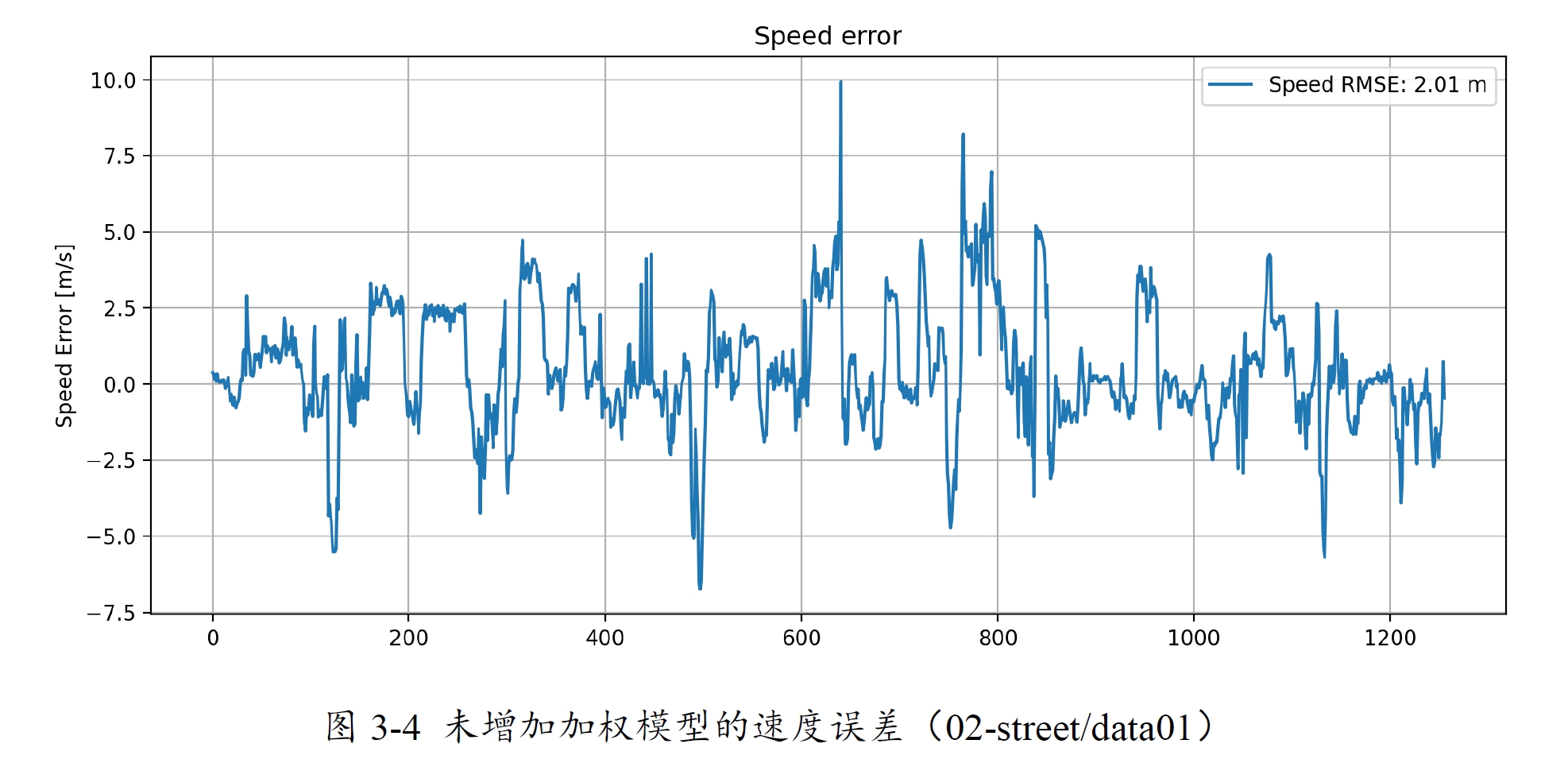
RTKLIB中的速度估计原本几乎没有进行加权，其表现的性能如图13-4所示，基本和等权差不多。

sig = (err <= 0.0) ? 1.0 : err * CLIGHT / freq;
var[nv] = SQR(sig);

原本加权方法的代码如上所示，其中的err由stats-errdoppler参数来控制。我在resdop中增加了新的加权方法，这里可以直接将伪距中的加权方法拷贝过来，并将原本的加权代码注释掉。

// resdop内部
prcopt_t opt_ = {0};
memcpy(&opt_, opt, sizeof(prcopt_t));
…
opt_.eratio[0] = 30.0; // doppler/phase error ratio
if (ssat)
    var[nv]=varerr(&opt_,&ssat[obs[i].sat-1],&obs[i],azel[1+i*2],sys);
else
    var[nv]=varerr(&opt_,NULL,&obs[i],azel[1+i*2],sys);
…
// 权的调节（修改H和v）
for (j=0;j<nv;j++) {
    sig=sqrt(var[j]);
    v[j]/=sig;
    for (k=0;k<4;k++) H[k+j*4]/=sig;
}

具体的，需要在resdop中增加var计算的代码，随后在resdop调用的地方进行加权操作。其中的opt_.eratio[0]表示stats-eratio1参数，它原本代表L1频点伪距误差相对于载波相位的缩放因子，因为varerr内部的模型是针对载波相位的。这里我拷贝了一份opt_，并以其中的opt_.eratio表示多普勒相对于载波相位的缩放因子，需要注意的是由于不再使用原本的加权方式，这就意味着stats-errdoppler参数将不再生效。

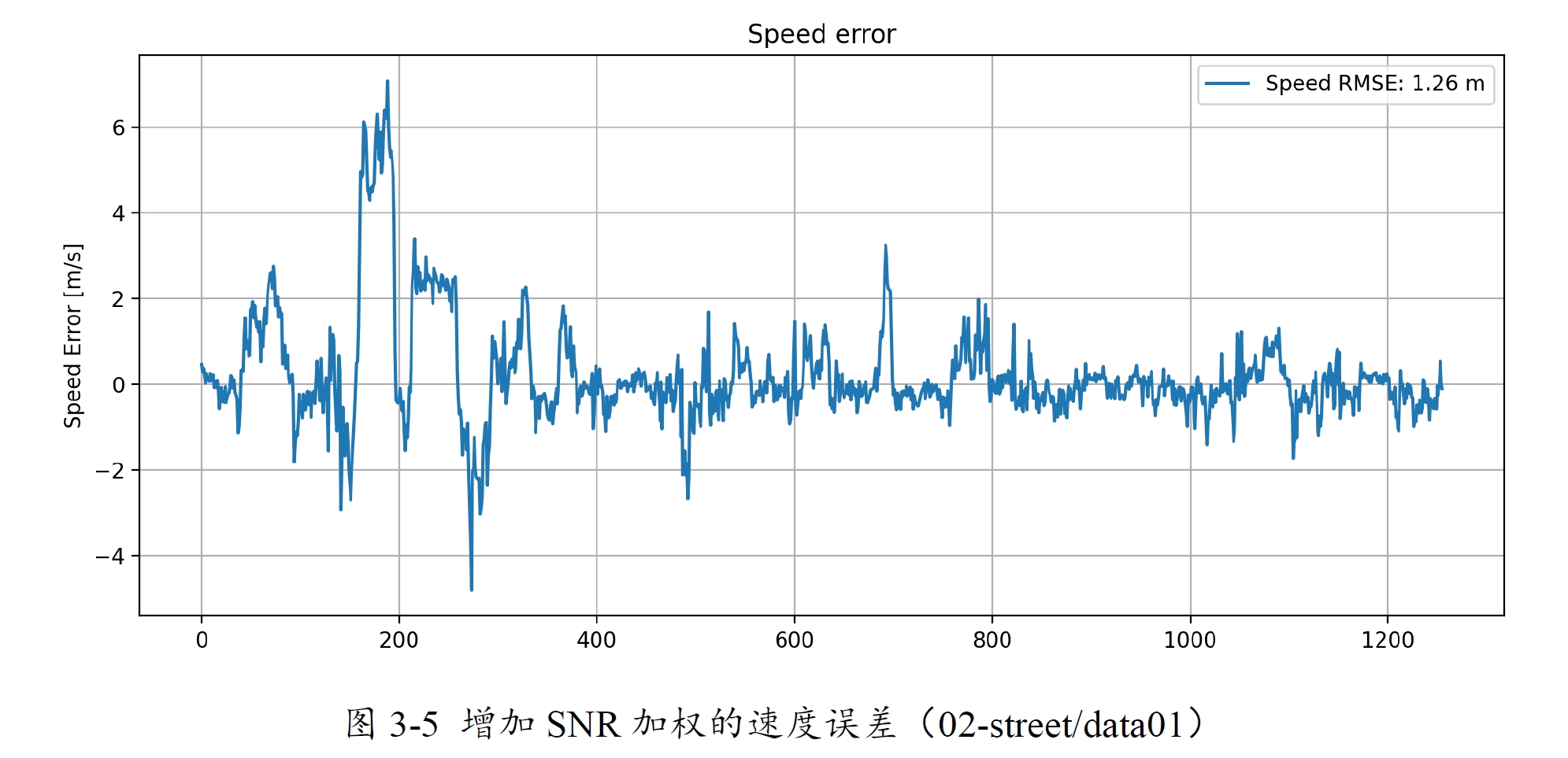
可以看到速度的误差水平有所降低。

11.2.3 M估计（抗差估计）

1. 原理与实现

M估计是一种广义的最大似然估计方法，旨在最小化一个目标函数，该函数对异常值不敏感。其核心思想是通过定义一个损失函数（或称为目标函数）来替代最小二乘法中的平方损失。

如果换一个角度来看M估计，可以认为它是一种更可靠的加权模型，该加权模型还利用到了验前残差（或新息），验前残差反映了预测与观测之间的差距，差距越小则给观测更大的权重，反之则给观测更小的权重。

M估计的数学表达如上所示。M估计的损失函数（或目标函数）通常包括Huber、IGG3和Tukey模型等，这里我主要关注其中的Huber和IGG3模型。

static int RobustLsq(const double *H, const double *v, int nx, int nv, double *dx, double *Q, double *var, int mode)

以上为实现M估计的C语言代码，需要注意：

• 迭代流程。迭代最小二乘，先计算权，再更新H和v；
• dx初值。初始的时候需要将dx赋值为0，不然结果可能会出现毛刺，本质是增加了迭代次数，以及位置首次迭代会除以残差本身。

2. 调参经验

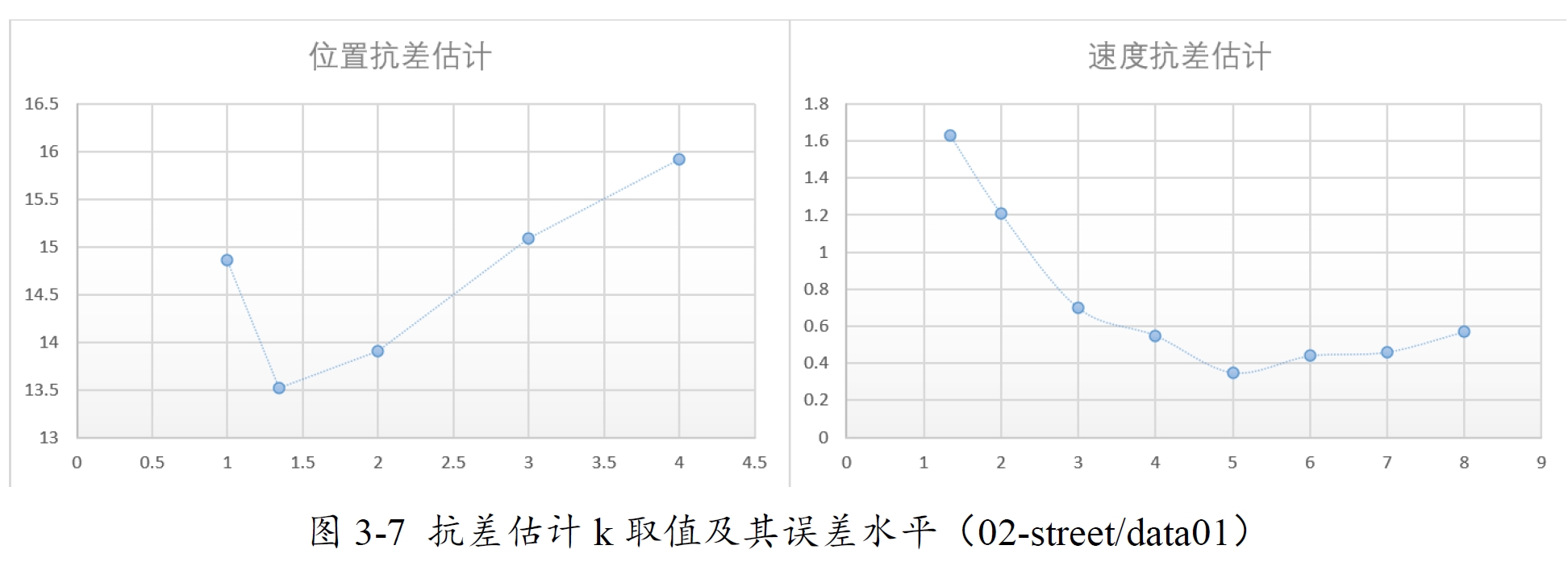
当前使用的Huber模型作为损失函数，位置抗差和速度抗差k的最佳取值是不同的，Huber模型中k默认为1.345，该取值对位置估计有效，但速度估计则需取值为5.0，k的取值更多的还是取决于测试数据所表现的残差水平，一般多试几次即可知道最佳取值。

当前场景中，IGG3模型没有很好用，尤其是IGG3的第三段，会导致一些残差较大但能正常运算的卫星失去作用，致使参与卫星过少，这主要是因为芯片中伪距中存在频繁的钟跳（参考2.5.2节）。

// 位置钟跳的粗略剔除
if (i == 0) AdjustClkJump(nv, H, x, v); /* median inner system as receiver clock */
 …
// 速度钟跳的粗略剔除
if (i == 0) {
    double med = DemianResOffset(v, nv, NULL, NULL);
    for (j=0; j<nv; j++) {
        v[j] -= med;
    }
    x[3] += med;
}

如果一定要使用IGG3模型的话，可以在使用前对所有残差数据扣除一个残差中位数（粗略代表钟跳），这样避免IGG3第三段操作时踢掉过多卫星；而Huber模型不需要扣除则是因为Huber不会剔除卫星，而迭代过程中则会消除钟跳误差。Huber等损失函数模型的实现请参考RobustWeightLsq，这里我是按照计算权值的方式对其进行定义的。

这里的Huber模型和IGG3模型的处理如下：

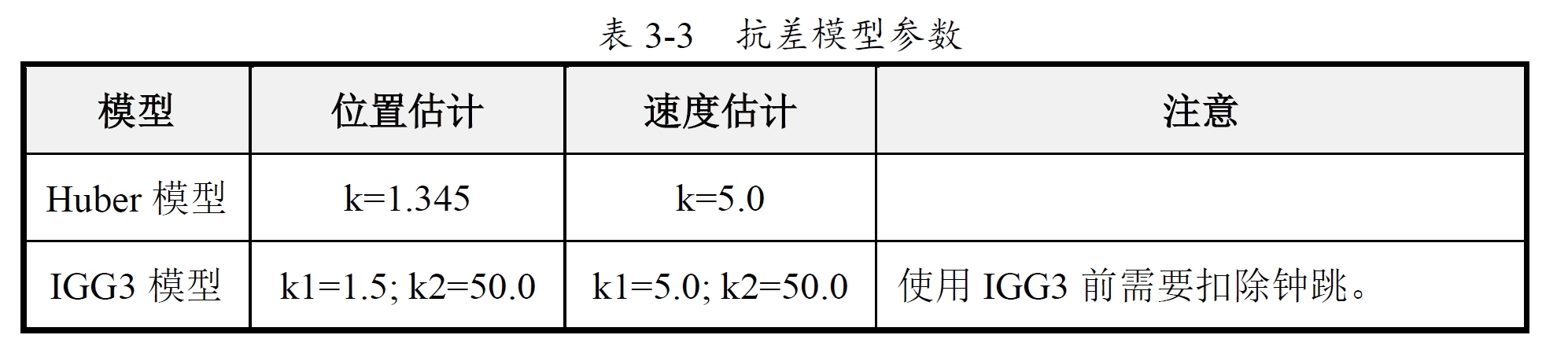
可以发现位置估计与速度估计时需要设置不同的参数，而IGG3模型由于面对的是整体残差较大的数据，因此k2需要设置得比一般情况更大的数值。

if ((mode==ROBUST_POS&&resid>=100) || (mode==ROBUST_VEL&&resid>=20)) {
    return 0.0001 / resid;
}

损失函数内部需要对残差较大的数据进行截断处理，即返回一个接近0的权值，另外不同算法的残差水平是不同的，需要设置不同的阈值（例如EKF中相应的部分需要设置为30、2）。

3. 测试结果

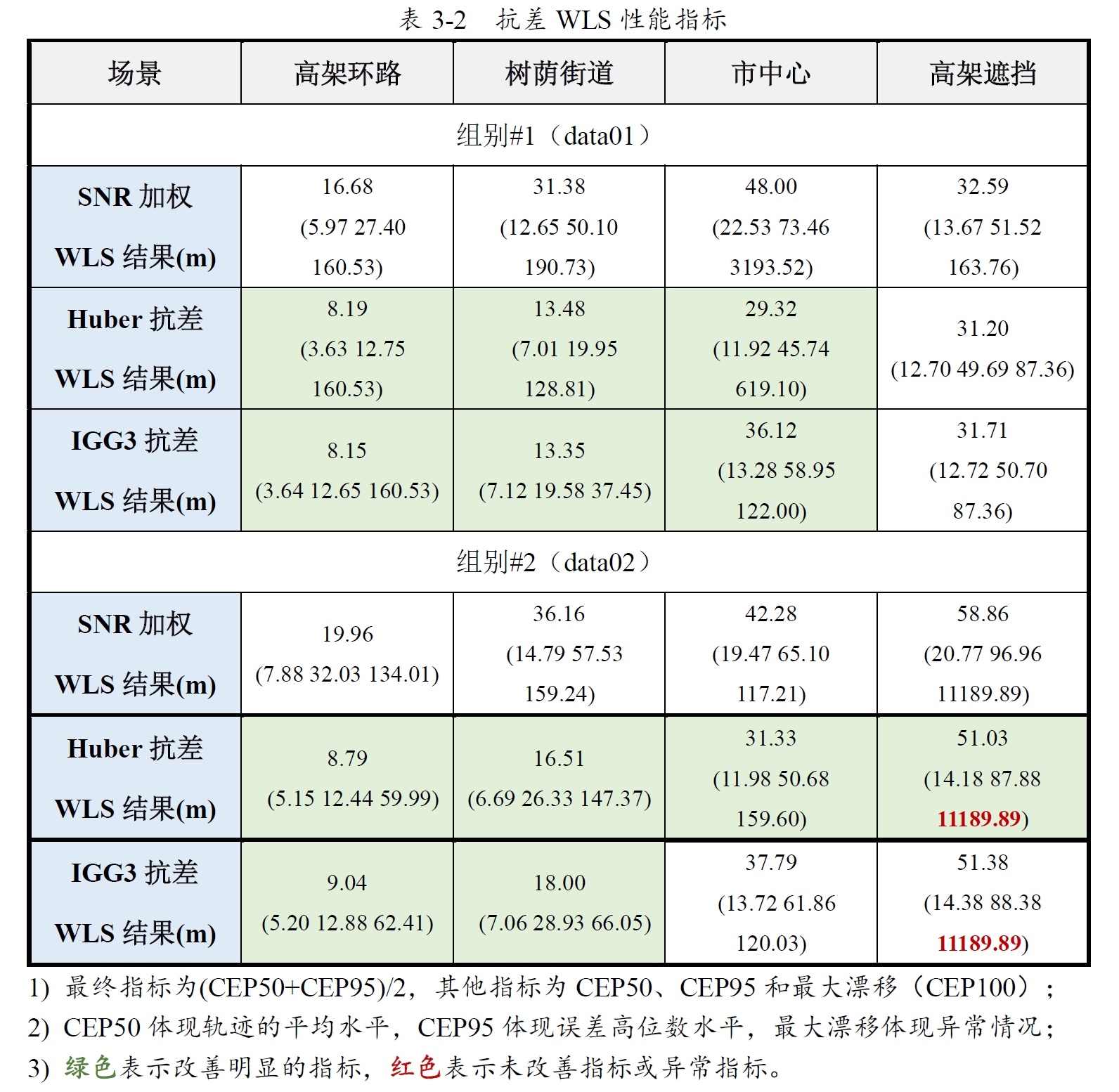
由上表可看到抗差最小二乘比单纯的SNR加权效果要很多。另外Huber的平均水平相较IGG3更好，而IGG3不会像Huber那样容易出现较大的异常偏差。

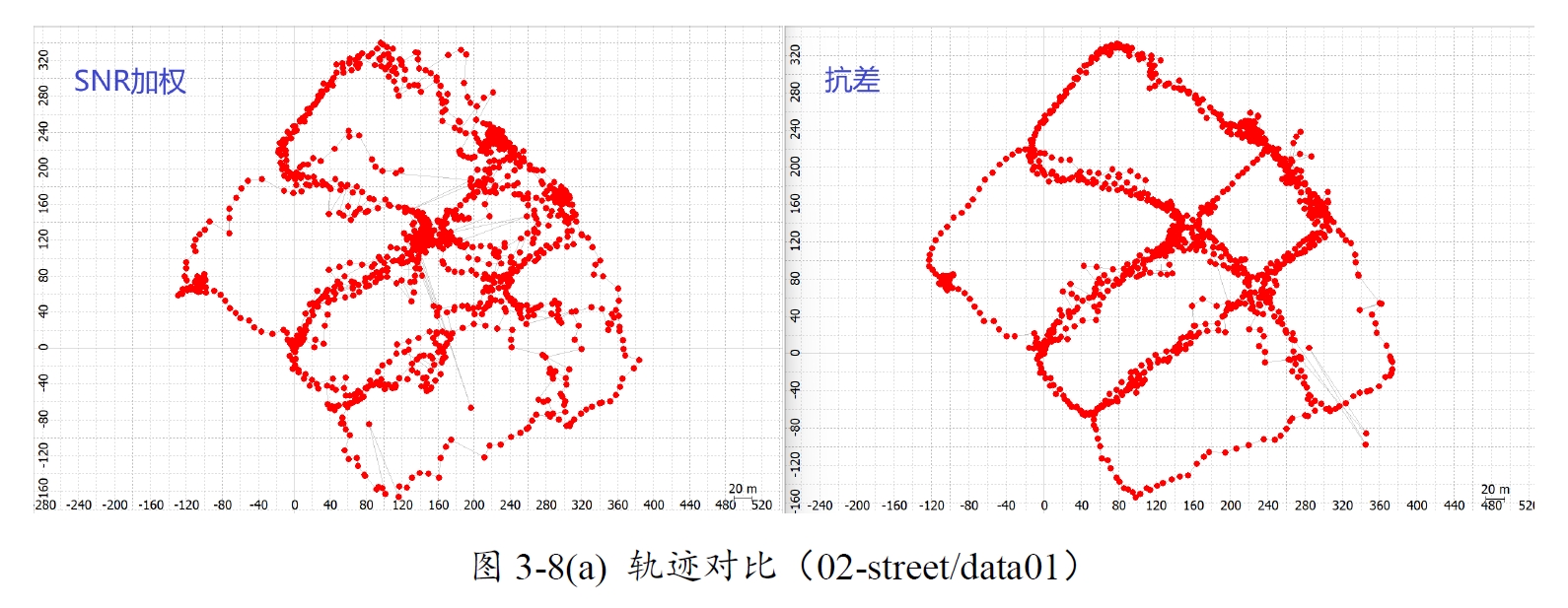
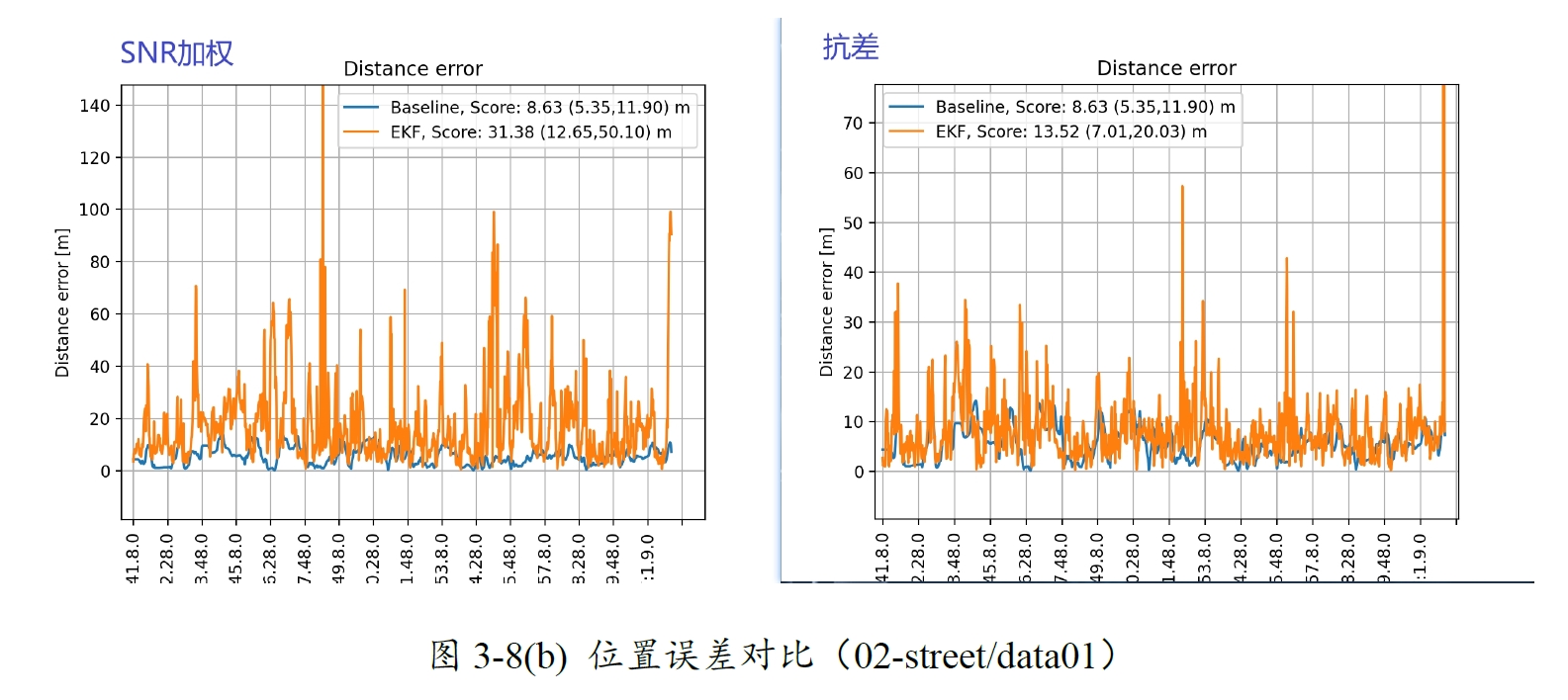
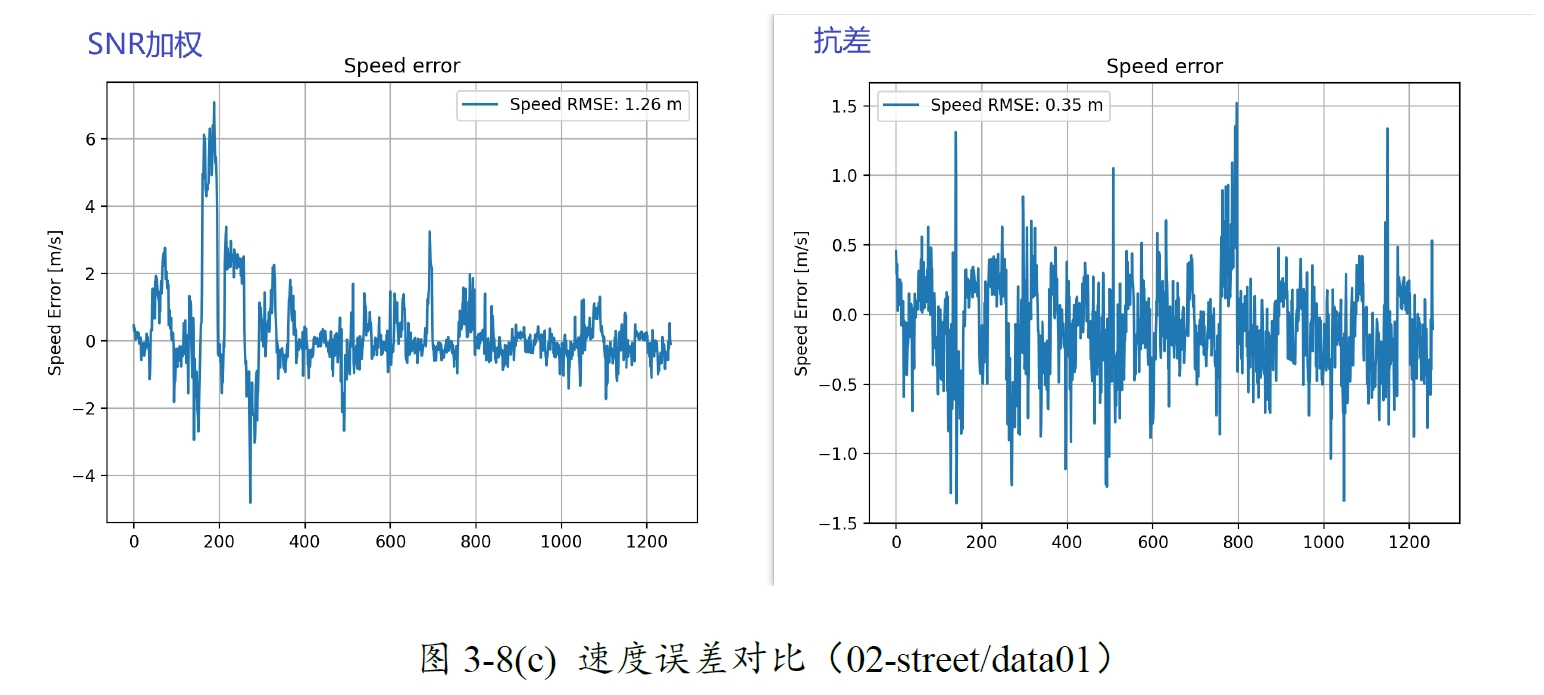
图13-8 SNR加权与Huber抗差对比（02-street/data01）

以02-street/data01组别数据为例，抗差后的结果所表现的性能提升了很多。

11.3 滤波器

11.3.1 参考卫星

RTKLIB原本的参考星直接采用模糊度列表中的第一颗卫星，可能存在不稳定性。这里修改了原本参考星选择的方法和条件，并且参考星会从浮点过程沿用至模糊度固定过程中。同时在参考星切换时，将单差模糊度做相应的换算，避免所有的模糊度历史信息直接丢失而全部重置。

可以尽量选择高度角最高并且无半周跳和周跳的卫星，并将参考星保存在refsatIdx[]数组中，在浮点滤波器/宽巷模糊度固定/窄巷模糊度固定中均采用相同的参考星，保持了一致性。

11.3.2 多普勒约束

时间更新过程时，添加了多普勒速度约束。如果上个历元的最终解为单点解或者DGPS解，这里就用通过多普勒最小二乘得到的速度对滤波器中的速度进行约束。这样可以避免上个历元的浮点滤波观测值过少导致的速度发生极端偏离的情况。

另外RTKLIB输出DGPS的情况较少，在没有固定的时候，基本以Float结果为主。可以卫星数过少的情况下，输出DGPS解状态。这样简单的进行精度的广义区分。因为目前的算法并没有将伪距和相位进行分开滤波，因此无法获得仅使用伪距解算的DGPS解。

11.3.3 抗差估计

ddres函数为计算双差残差的函数，验前残差（新息）与验后残差会共用该函数。在验前条件下，增加了抗差部分。依据残差采用IGG3模型调整观测协方差阵R阵，并且在残差普遍较大的情况下，同时调整状态协方差阵P阵，认为此时预测并不准。在验后则不进行这些操作。

1. 调整R阵

这个过程是单独针对少量观测值产生误差的情况。当单个观测值误差产生时，相应的残差v的值会明显增大。因此我们依赖残差v对每个观测值进行判断是否符合预期，当不符合时即采取降权的方法。

用HPHT+R与v的比值来确定R阵放大的倍数,采用IGGⅢ模型，由于这里是双差方程，针对单颗卫星的做法是仅放大单颗卫星的R，当系统内卫星超过半数都存在偏差时，可以认为参考星可能存在问题，此时对所有相关的协方差也要进行放大。

2. 调整Q阵

另外针对所有或者绝大多数残差值都很大的情况，此时可能并不是由于单个观测值产生了误差，而是预测值本身不准造成的。因此我们应当对滤波器的状态量的协方差进行放大，以反映预测值的不准确。

用残差v的平方和与HPHT+R的迹的比值来衡量状态量协方差阵的不符合程度。对于超出阈值k0的情况，需要对P阵整体放大alpha/k0倍，以降低滤波器对预测值的依赖程度。

11.3.4 航向约束

方法一：调整滤波器进行航向约束。航向约束只需要在观测向量z中增加航向观测即可，同时对H阵进行调整，不过该方法可能作用不大，至于基于后文的设计是无效的，暂不确定是否有更合适的方法。

方法二：调整量测更新的改正数。修改量测更新中的x += Ky，对其中的Ky进行侧向偏移判断，如果偏移较大的话，则进行修正，该方法经过验证是有效的。

方法二较为简单，下面对方法一进行介绍，其中预测阶段的内容与原先保持不变。

1. 观测模型

观测向量包括伪距、多普勒和航向：

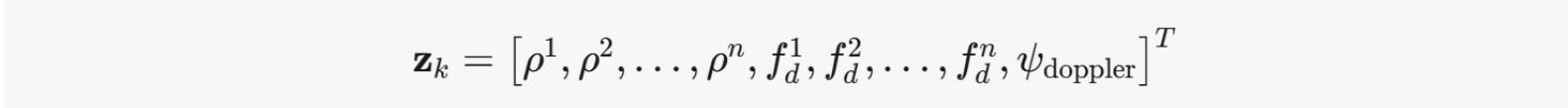
1）伪距观测

2）多普勒观测

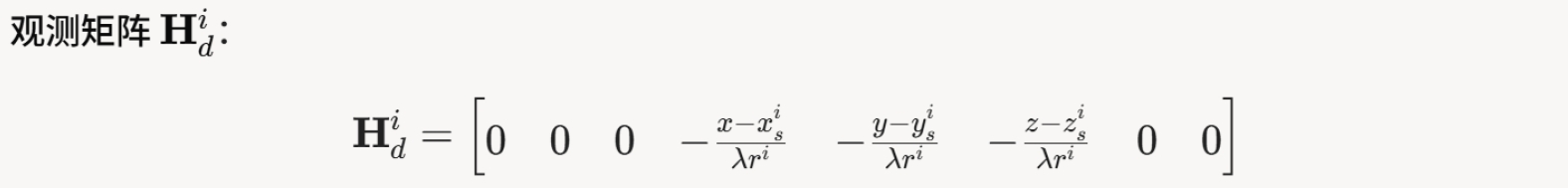
3）航向观测

航向从多普勒速度估计，基于ENU坐标系下的东向和北向速度分量。

注意：这里需要将ECEF速度转换为ENU速度。

观测方程为：

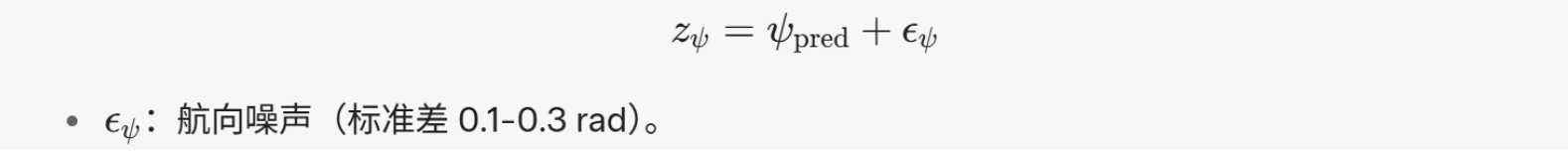
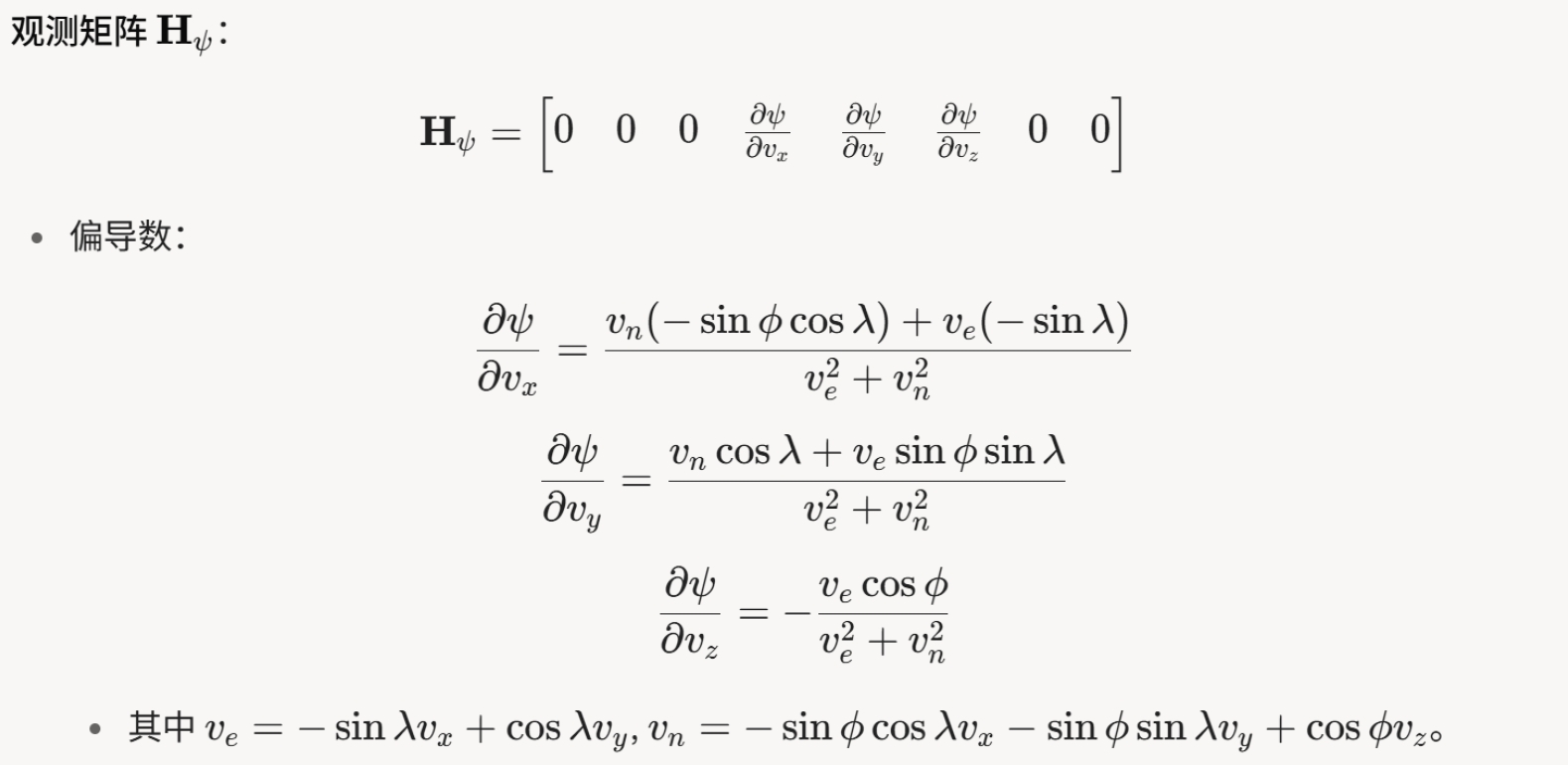
2. 观测噪声协方差

观测噪声协方差矩阵 R 描述伪距、多普勒和航向观测的不确定性。这里我们主要观测其中的航向噪声。航向噪声如果设定得不好，通常会让滤波器崩溃：

航向噪声方差，动态计算以反映速度对可靠性的影响：

3. 代码实现

if (stat > SOLQ_NONE && sol_lsq.ns >= 5 && (fabs(enu2[0]) >= 0.5 && fabs(enu2[1]) >= 0.5)) {
    ecef2pos(sol_lsq.rr, pos1);
    ecef2enu(pos1,sol_lsq.rr+3,enu1);
    psi_doppler1 = atan2(enu1[0], enu1[1]);
 
    ve = enu1[0];
    vn = enu1[1];
    
    ParPsi(ve, vn, pos1, par_psi); // 航向观测矩阵 H
 
    for (j = 0; j < 3; j++) {
        H[j + 3 + nv * NX_F] = par_psi[j];
    }
    v[nv] = psi_doppler1 - psi_doppler2; // OMC
    vm = sqrt(SQR(enu1[0]) + SQR(enu1[1]));
    var[nv] = SQR(0.05) + (SQR(1)-SQR(0.05) * exp(-vm/0.5));
    nv = nv + 1;
} else {
    // 当航行观测缺失或不可靠的时候，直接跳过该历元的航向观测，并移除v、H、R中的相关信息
    nv = nv;
}

11.3.5 高程约束

原理类似航向约束，不过同样效果不是很显著。

采用约束高程、约束U向的速度加速度等方法。当时系统运行场景非常平坦时候，采用绝对高程进行U向的约束（哪怕是较紧约束，效果也比较一般）。

具体实现上，增加虚拟观测方程，对filter对rtk->x与rtk->P进行约束。其中对U方向位置的约束，则是采用参考结果转到ENU方向并且只对U方向位置进行约束。或者采用实际的高程值，构建U方向位置的方程进行约束。

对速度的约束则是，认为行进过程中U方向的速度为0，给定R=SQR(0.001)来构建虚拟观测方程，每个历元对U方向的速度进行约束。对速度和加速度的约束分两步，认为运动中U方向的速度和加速度都为0，给定R=SQR(0.001)，分别构建两个虚拟观测方程，从而达到约束U方向速度/加速度的作用。

上述的方法最终希望达到对浮点解U方向高程进行控制，使得历元间的高程之间形成约束。实际使用这些方法后，高程方向位置的稳定性的确得到了控制，但是对与平面的位置没有明显的作用。这可能本质上是由于滤波过程中，U方向的位置与平面位置之间的关联性并不强，最终导致即便是采用极端的固定值约束高程，水平位置也没有更好地往正确的位置收敛。

11.4 模糊度固定

在模糊度固定的流程上进行了一些调整。大体上是按照先固定宽巷模糊度，再固定L1/L2/L5模糊度的方式进行固定，另外采用了部分模糊度固定的方式。

11.4.1 增加宽巷模糊度固定流程

新增了宽巷模糊度固定流程。宽巷模糊度波长更长，理论上更容易固定为整周。在宽巷模糊度的约束基础之下再去固定L1/L2/L5的模糊度理论上也会更加容易。另外宽巷模糊度的固定也可以作为后续模糊度固定的控制条件。

目前双频的宽巷模糊度固定manage_amb_wl_LAMBDA与hold模糊度holdamb_wl的频点要输入参数进行控制，其中(0,1)作用于L1/L2双频固定，(0,2)作用于L1/L5双频固定。

11.4.2 部分模糊度固定

1. 基于方差的部分模糊度固定

这里的方差指的是双差模糊度状态验后的P，其代码流程如下：

1. 执行resamb_LAMBDA_par_new函数
2. 使用其中的sort_idx对P值（Qb=D*Qc*D'）大小进行排序
3. 随后在循环中剔除P中较大模糊度，这里使用了QQb=Qb*1000，为的是方便观察：
for (int iter = 0; (iter < nb / 3 || iter < 3); iter++) {…}

在做部分模糊度固定时，采用的基础循环框架是，当lambda失败时，则剔除一个模糊度重新进行固定。一般按照模糊度的方差P来决定剔除顺序，优先剔除方差较大的模糊度，这些模糊度被认为经过浮点滤波器未得到精确估计，可能造成后续的lambda失败。这个过程最少进行三次，最多去掉1/3向下取整的模糊度数。

这个方法目前只应用在了窄巷模糊度固定中。因为满足条件的宽巷模糊度本身就比较少，做剔除的意义不大，可能会导致固定很少的模糊度，得到一个精度很低的宽巷固定解；加之过多循环也会影响算法效率。

2. 基于多解融合的部分模糊度固定

该方法基于的思考是：认为模糊度收敛在了一个局部区域，导致最优/次优解比较接近，这么描述不一定精准，但是可以简单这么理解。

对于每个确定的待估计模糊度组，我们仍然基于lambda方法进行整周固定，并依据最优解/次优解/第三优解这三个解的结果和ratio值进行综合操作。对于每次循环，待固定模糊度个数nb_=nb-iter。如果ratio>Max_thresar，则认为全部的nb_个模糊度固定成功，此时的最优解即为正确解；如果Max_thresar>ratio>nb_thresar（nb_thresar根据模糊度数量nb_确定），则接受其中的部分模糊度作为正确的模糊度，条件是：

• 最优解中与上历元正确模糊度相等的模糊度
• 最优解与次优解相等，并与浮点模糊度差值在4以内，同时ratio[1]>Min_thresar
• 最优解、次优解与第三优解一致，并于浮点模糊度差值在4以内，同时ratio[1]>nb_thresar 且ratio[2]>Min_thresar

以上任一条件满足的话，则考虑该模糊度是OK，然后再来看有多少OK的模糊度，如大于85%。

类似于ratio值表征最优解与次优解的差异，这里增加了ratio[1]和ratio[2]表征次优解与第三优解的差异，第三优解与第四优解的差异。习惯地认为，与后一组解差异越大（存在断崖式差异）的解的可信性会更高。例如当ratio[2]足够大的时候，我们认为s[0]/s[1]/s[2]三者接近但s[3]与前三者差异很大，那么尽量去前三个解中找共同的部分进行固定。

// resamb_LAMBDA_par_new
函数内部
// s[]
可以简单理解成从浮点到整数的改正数，而第二个条件是当前计算的 ratio
大于自适应模糊度阈值（此时认为模糊度固定成功了一般）
//
当前版本代码使用的是最优/
次优前 80%
的模糊度作为多解融合的基准
else if (s[0] <= 0.0 || rtk->sol.ratio[1] > rtk->sol.thres[1])

由于这种固定方法存在一定的风险，因此都限制了整周与浮点模糊度的差值在4以内。最终认为正确的模糊度数量必须在nb_的85%以上，才得到最终正确的模糊度。

同样的法二在宽巷模糊度固定和窄巷模糊度固定中的条件/参数等等的设置亦有不同，在此不对细节多做赘述，整体的思想内核是一致的。

其他启发：

• 模糊度是一组一组，而不是选取每个模糊度单独的最优解来作为最优组合。只是一种感觉，而专业的描述。
• 模糊度收敛在了一个局部区域，导致最优/次优解比较接近，这么描述不一定精准，但是可以简单这么理解。

11.4.3 demo5中的部分固定

原本的模糊度固定本身有两个部分控制的方法：

1. 加入卫星的动态调整与错峰固定

其一是如果当前历元新增的卫星使得模糊度固定失败并且造成ratio大幅的下降，则将新加入的卫星按一定的顺序，通过调整nlock至负数的方式，使这些卫星可以错开加入滤波或固定，并且重新进行模糊度固定，这样做可以避免对滤波器的稳定性造成冲击，使得出现长时间难以固定的状况。该方法的优点是可以针对新加卫星过多难以固定的问题，同时缺点是一方面卫星的加入顺序会形成一定程度的不可控性，缓慢加入也不一定能够彻底解决无法固定的问题，另外一方面新加卫星数很多的情况往往是在短暂遮挡后卫星重新观测到，这样卫星缓慢的加入会导致待固定模糊度个数缓慢的上升，往往重固定也会变慢很容易超过10s以上。

2. 随机剔除卫星以优化ratio值

其二是如果模糊度个数足够但是ratio值检验不通过导致不固定，这时候会随机删除一个卫星使其不参与固定，并对他的nlock也置为负数。这个操作有些类似pntpos的raim环节，这里仅随机删除一个但不会进行循环。同样可能带来的负面影响也是容易给算法带来不确定性。

11.4.4 其他注意事项

另外在模糊度固定方面还有可以进一步的操作。例如在完成了初次的模糊度固定以后，还可以利用模糊度固定后的结果，对未成功固定的模糊度进行一轮固定，扩大固定的模糊度组，这样能够更大程度的抵御频繁遮挡的环境。

/* adjust non phase-bias states and covariances using fixed solution values */
if (!matinv(Qb,nb)) {  /* returns 0 if inverse successful */
    /* rtk->xa = rtk->x-Qab*Qb^-1*(b0-b) */
    matmul("NN",nb,1,nb,Qb ,y,db); /* db = Qb^-1*(b0-b) */
    matmulm("NN",na,1,nb,Qab,db,rtk->xa); /* rtk->xa = rtk->x-Qab*db */
    
    /* rtk->Pa=rtk->P-Qab*Qb^-1*Qab') */
    /* covariance of fixed solution (Qa=Qa-Qab*Qb^-1*Qab') */
    matmul("NN",na,nb,nb,Qab,Qb ,QQ);  /* QQ = Qab*Qb^-1 */
    matmulm("NT",na,na,nb,QQ ,Qab,rtk->Pa); /* rtk->Pa = rtk->P-QQ*Qab' */
    
    trace(3,"resamb : validation ok (nb=%d ratio=%.2f thresh=%.2f s=%.2f/%.2f)\n",
            nb,s[0]==0.0?0.0:s[1]/s[0],rtk->sol.thres,s[0],s[1]);

    /* translate double diff fixed phase-bias values to single diff
    fix phase-bias values, result in xa */
    // 调用restamb()，重新存储单差的模糊度
    restamb(rtk,bias,nb,xa);
}

注意：RTKLIB-Demo5最终固定以后，会通过一些操作，得到最终的位置和误差协方差矩阵。也可以使用filter（量测）完成同样的工作，不过这里这里会减少计算量。

11.5 其他调整

11.5.1 卫星较少时的异常处理

卫星数过少的情况下，输出DGPS解状态。这样简单的进行精度的广义区分。因为目前的算法并没有将伪距和相位进行分开滤波，因此无法获得只使用伪距解算的DGPS解。