附录E. 模型与算法
E.8 精密单点定位
在 PPP 模式下,RTKLIB 同样采用与附录 E.7 中描述的方案类似的扩展卡尔曼滤波(EKF)。与相对定位不同的是,PPP 采用了类似于单点定位模型的非差(ZD)观测方程,而不是双差(DD)观测方程。
E.8.1 PPP 非差观测模型(ZD)
利用式 (E.3.4) 和 (E.3.2),卫星 s 的无电离层 LC 载波相位距离 和伪距 观测可表示为:
其中,通过形成 E.5 (7) 中描述的无电离层 LC 组合,消除了式 (E.3.4) 和 (E.3.2) 中的电离层项。 是以米为单位的载波相位偏差, 是 和 的无电离层 LC 载波相位改正项,表达式如下:
E.8.2 接收机天线相位中心模型
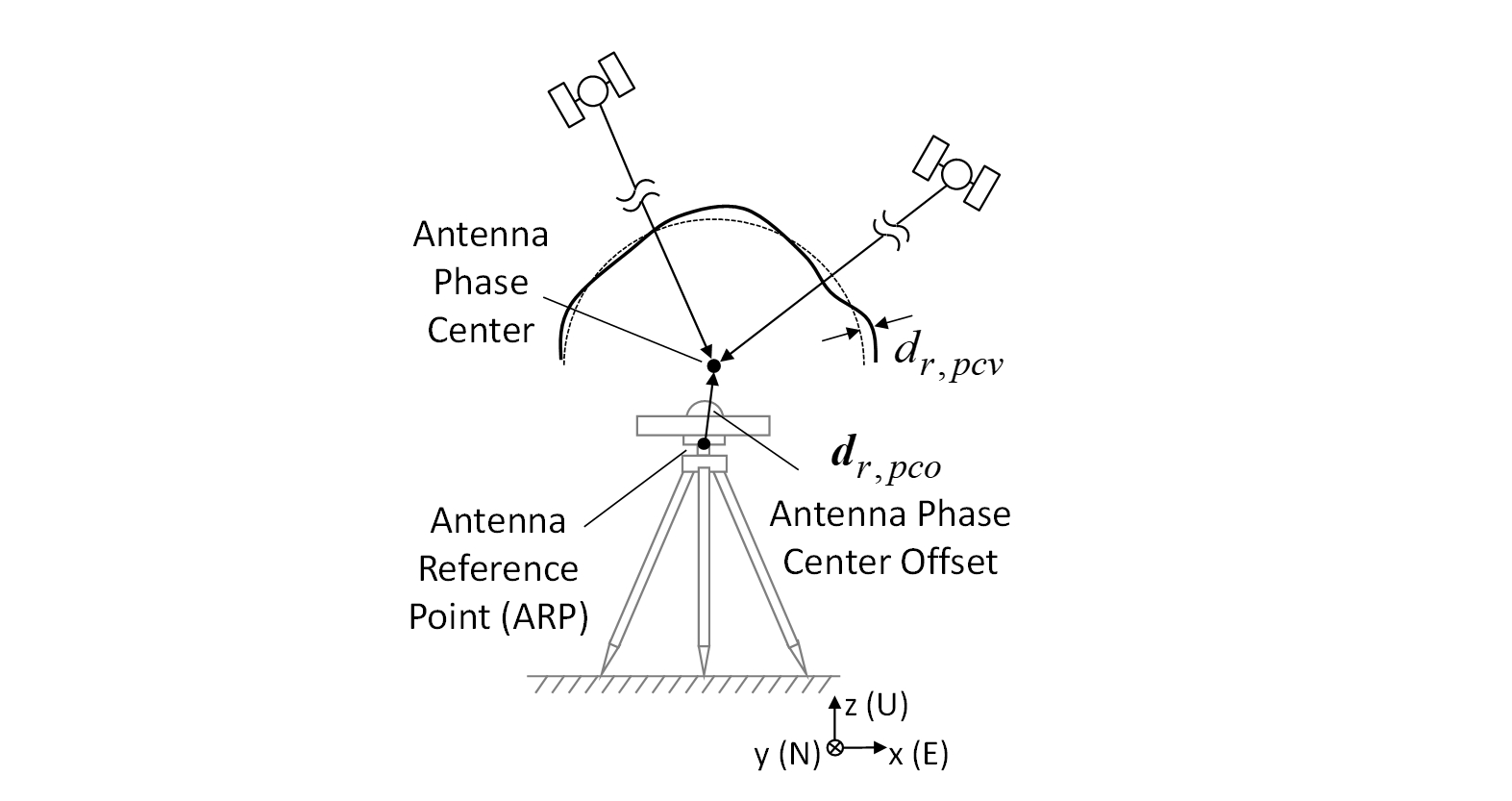
图 E.8-1 展示了接收机天线的 PCO(相位中心偏移)和 PCV(相位中心变化):
- PCO 定义为接收机天线相位中心相对于ARP(天线参考点)的相对位置。
- PCV 定义为天线因仰角和方位角而产生的额外相位延迟。
各种天线类型的 PCO 和 PCV 值已通过适当的天线校准过程进行测量,并以一些标准格式的文件呈现给用户。当前版本的 RTKLIB 支持用于包含 PCO 和 PCV 数据的天线模型的 NGS PCV 和 ANTEX 格式。PCO 值通常以接收机位置的本地坐标给出。因此,接收机天线在 ECEF 坐标系下的 波段 PCO 表示为:
其中 是由式 (E.2.10) 给出的从地心地固(ECEF)坐标系到本地坐标系的旋转矩阵, 是用本地坐标系表示的 频段接收机天线相位中心偏移(PCO)。仰角为 时 频段接收机天线相位中心变化(PCV) 可根据给定的不同仰角下的 PCV 值通过线性插值得到,如下所示:
其中 。
图E.8-1 接收机天线相位中心
E.8.3 卫星天线相位中心模型
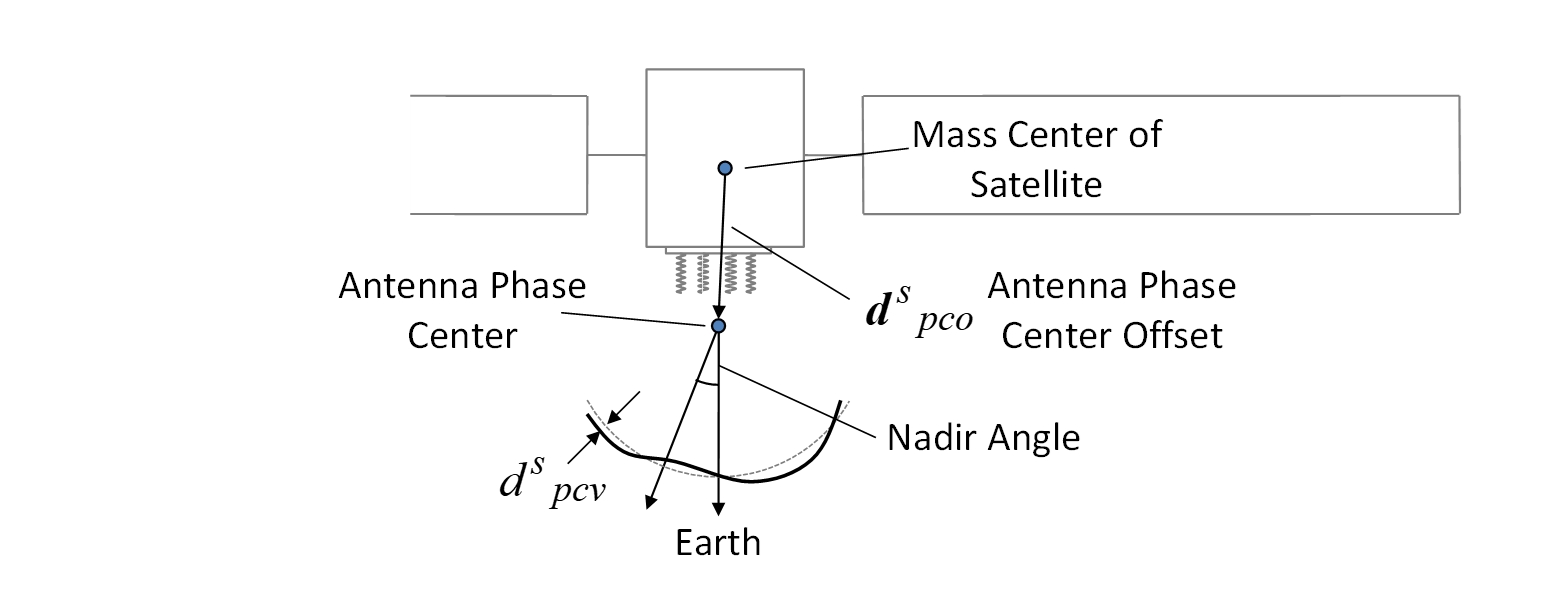
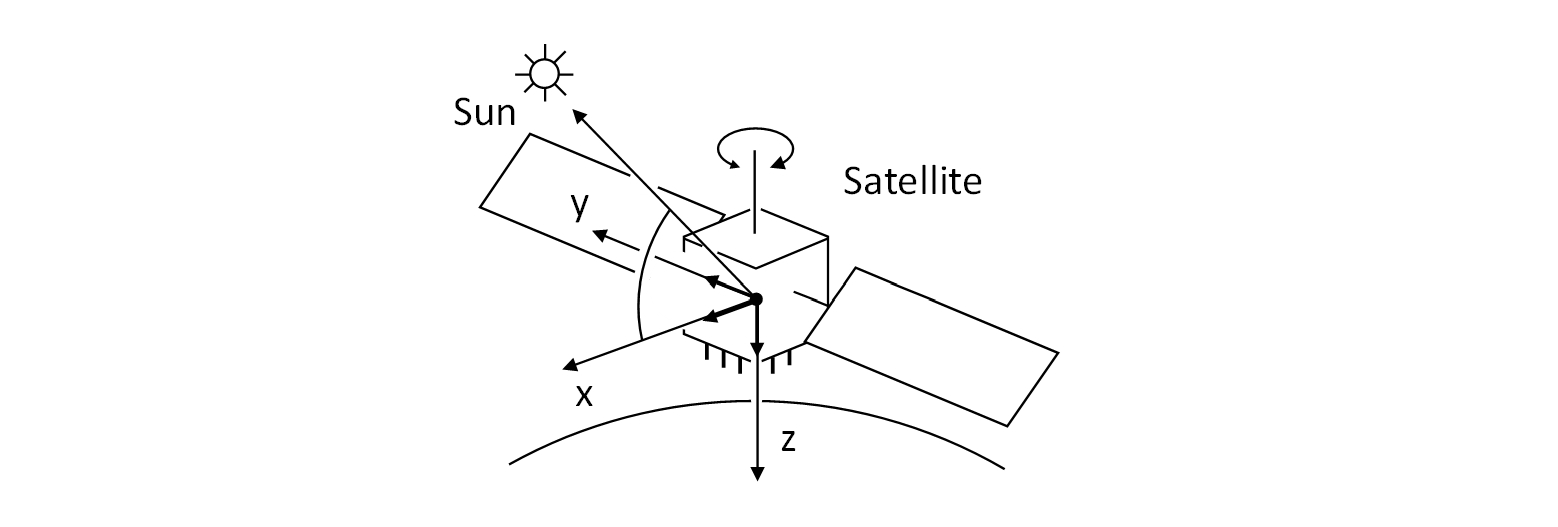
图 E.8-1 展示了 GNSS 卫星天线的 PCO 和 PCV,与接收机天线类似,这些数据通常也由 IGS(国际GNSS服务组织)以 ANTEX 文件的形式提供。RTKLIB 也可以导入此类卫星天线模型。卫星天线的 PCO 通常以相对于卫星质心(CoM,center of mass)的卫星固连坐标给出,如图 E.8-3 所示。因此,卫星固连坐标系下的卫星天线 PCO 需要转换到地心地固(ECEF)坐标系下。PCV 也以天底角(nadir angle)来表示。
图E.8-2 卫星天线相位中心
图E.8-3 卫星固连坐标系
假设采用标准卫星姿态控制模式,从卫星固连坐标系到地心地固(ECEF)坐标系的坐标转换矩阵 如下所示:
其中 是太阳在地心地固(ECEF)坐标系下的位置。天底角 也可推导如下:
E.8.4 地球潮汐引起的测站位移
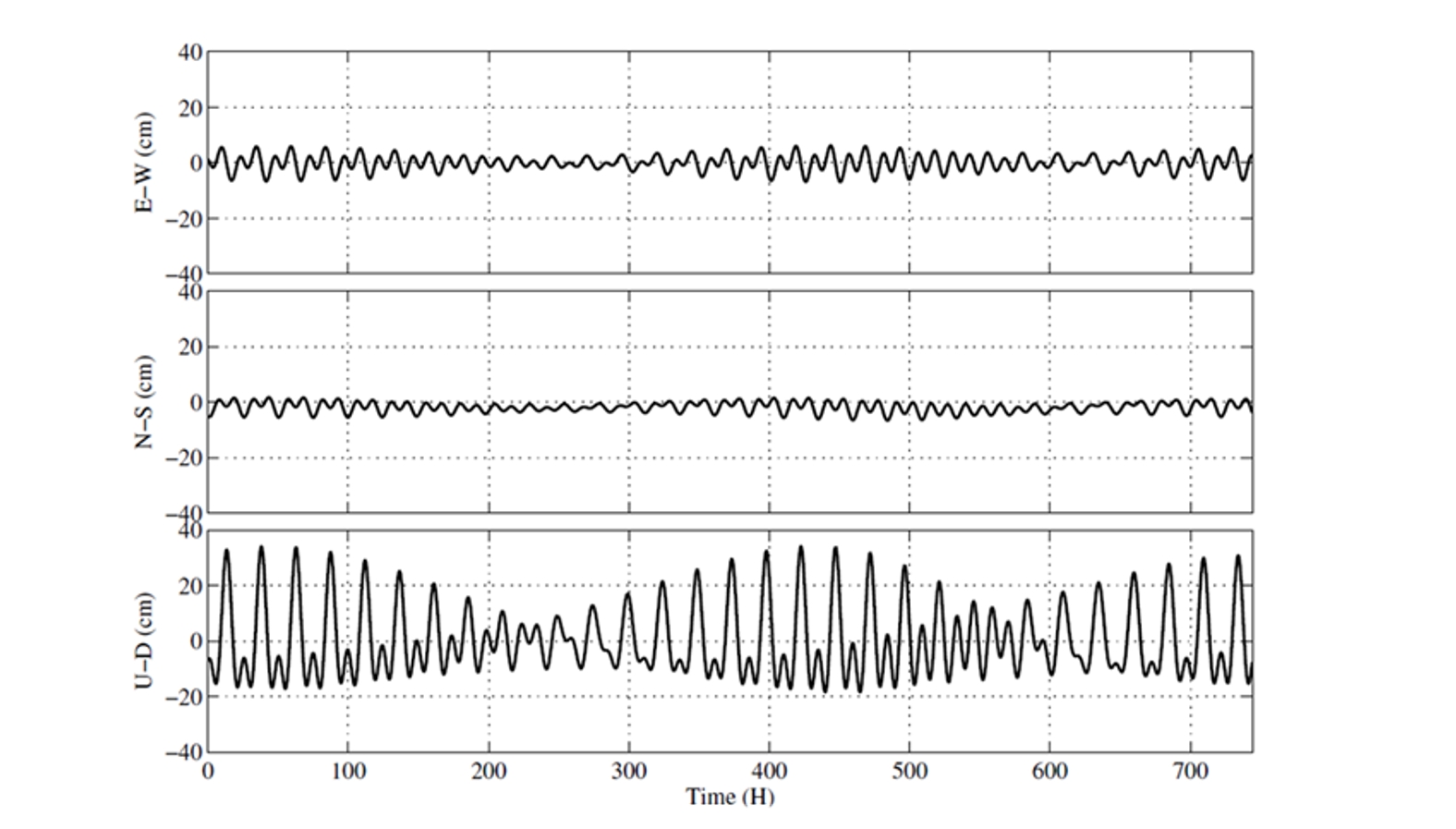
固定在地面上的接收机位置会受到地球潮汐效应的影响。在基线分析中,潮汐效应通常会被忽略,因为双差(DD)几乎可以消除所有这些效应。然而,在精密单点定位(PPP)模式下,该效应所引起的误差需要考虑到模型中,因为其垂直分量的振幅有时可达几十厘米。图 E.8-2 展示了地球潮汐引起的测站位移效应示例。
图E.8-4 Displacement by Earth Tides
E.8.5 相位缠绕改正
相位缠绕效应是由接收机天线和卫星天线之间的相对旋转引起的相位超前和延迟。相位缠绕建模如下:
其中 为整周模糊度,其取值应确保避免周跳。
E.8.6 使用 PPP 估计 接收机位置
通过使用扩展卡尔曼滤波(EKF),精密单点定位(PPP)情况下的未知状态向量 确定如下:
其中 为天顶总延迟(ZTD,zenith total delay), 和 分别为对流层梯度的北向和东向分量。 为非差(ZD,zero-differenced)无电离层 LC 载波相位偏差(单位:米)。
观测向量 同样根据式 (E.5.21) 和 (E.5.22),由非差无电离层 LC 相位距离和伪距观测值定义为:
其中:
观测模型向量 和偏导数矩阵 可表示为:
其中:
: 载波相位观测误差的标准差(m)
: 伪距观测误差的标准差(m)
利用 EKF 公式以及附录 E.7 中描述的类似时间更新过程,可估计包括接收机位置和速度、接收机钟差、对流层参数以及无电离层 LC 载波相位偏差在内的未知参数。
请注意,与相对定位情况类似,为了解决载波相位偏差中的整周模糊度问题,需要卫星端的 FCB(小数周偏差)附加信息。这一过程有时被称为 PPP-AR(模糊度解算)。当前版本的 RTKLIB 仅支持法国国家空间研究中心(CNES)提供的宽巷 FCB 和 IRC(整周恢复钟)产品。该实现尚处于试验阶段,并不稳定。仅在事后处理模式下,将处理选项 “Integer Ambiguity Resolution(整周模糊度解算)” 设置为 “PPP-AR” 时,才会启用 PPP-AR 功能。
