附录E. 模型与算法

E.3 信号测量模型

E.3.1 GNSS信号结构

图E.3-1展示了一个典型的GNSS信号结构。GNSS信号通常由载波（Carrier）、伪码（Code）和导航数据码（Data）的乘积组成。具体的，伪码和数据码一起先通过调制而依附在正弦波形式的载波上，然后卫星将调制后的载波信号播发出去。

GPS、GLONASS、Galileo、QZSS、北斗和SBAS提供的GNSS信号详细规格可以在附录G中找到。

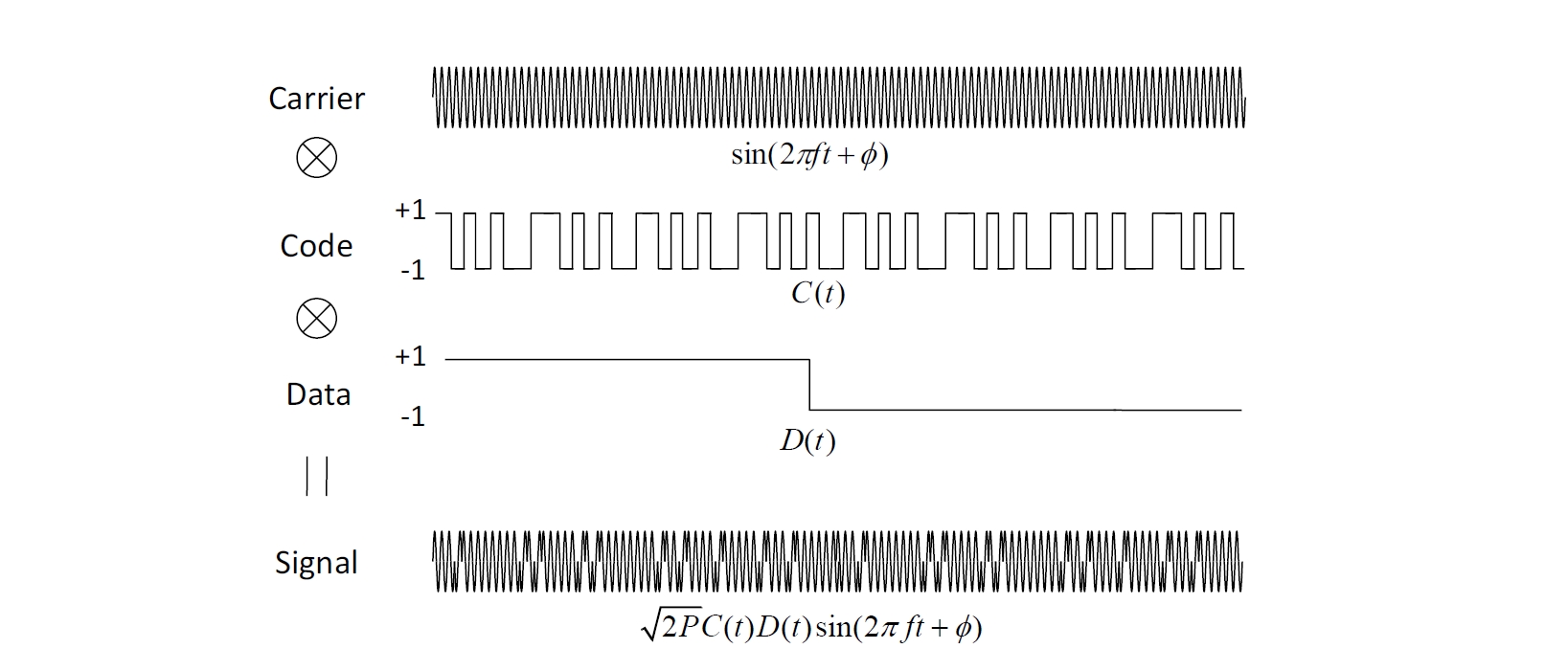
图E.3-1 GNSS信号结构

E.3.2 伪距测量模型

伪距指的“接收机天线到卫星天线之间的距离，其中包含了卫星钟差和接收机钟差（及其他偏差，如大气层延迟）”[9]。频段的伪距 可以用接收机测量的信号接收时间 和卫星测量的信号发射时间 来表示：

该方程也可以用卫星与接收机天线之间的几何距离 ，接收机和卫星的钟差 、，电离层和对流层延迟 、，以及测量误差 来表示：[64]

图E.3-2 伪距模型

E.3.3 载波相位测量模型

“载波相位其实是测量卫星发来的信号载波和接收机自己产生的参考信号之间的一种节拍差（beat frequency）”[9]。频段的载波相位 可以表示为：

其中， 是初始时间（s）， 是接收机本地振荡 频段的相位（cycle）， 是 时刻发射的导航信号的 相位（cycle）。 是接收机本地振荡器在 时刻的 初始相位（cycle）， 是 时刻发射的导航信号的 初始相位（cycle）。

相位距 定义为载波相位与载波波长 （m）的乘积，也可以通过载波相位偏差 和载波相位校正项 来表达，后者包括天线相位中心偏移和变化、地球潮汐导致的站点位移、相位缠绕效应以及卫星钟的相对论校正：

其中：

通常被称为载波相位整数模糊度、载波整周模糊度或简称为模糊度。有关载波相位校正项的详细公式，请参考附录 E.8。

GPS L1频段的载波波长是19cm，为什么通常说载波相位的测量精度是cm或mm级别？

虽然 L1 载波的波长是 19 cm，但测量精度远高于波长，这是因为载波相位测量的精度取决于相位分辨能力，而不是波长本身。

接收机的相位测量是通过接收机锁相环实现的，它能分辨非常小的相位变化，实际测量精度通常在 0.01 周期左右（即1.9mm），主要受噪声和硬件限制。

E.3.4 卫地距（接收机与卫星天线）

接收机与卫星天线几何距离（卫地距）指卫星天线（相位中心）与接收机天线（相位中心）在惯性坐标系中的物理距离。首先，信号传输时间 可以通过以下方式推导出来：

方程的两边都包含了 。因此，需要进行几次迭代来解这个方程。几何距离可以通过 ECEF坐标系中 时刻的接收机位置 与 时刻的卫星位置 来表示：

其中， 是 时刻从 ECEF（地心地固）到 ECI（地心惯性）坐标系的转换矩阵。为了在 ECEF 坐标系中表达几何距离，需要考虑地球自转效应以获得几何距离。该方程可以用以下方程之一近似，精度在1毫米级别以内。当前版本的 RTKLIB 使用方程 (F.3.8b) 来计算几何距离。(F.3.8b) 中的最后一项有时被称为萨格纳克效应（Sagnac effect）。

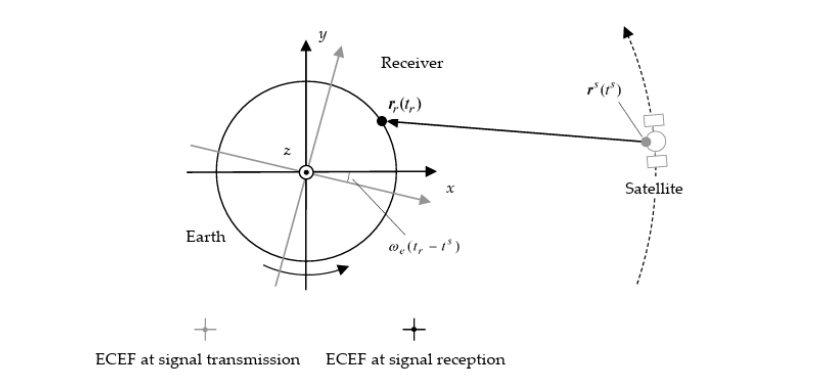
图E.3-3 几何距离和地球自转校正

E.3.5 卫星方位角与仰角

接收机到卫星的单位视距（LOS）向量在 ECEF（地心地固）坐标系中可以表示为：

在方程中，忽略了地球自转效应。从接收机到卫星方向的方位角 和仰角 可以从以下公式推导出来：

其中， 是从 ECEF 坐标系到接收机位置的局部坐标系的坐标旋转矩阵。有关该矩阵的详细形成，请参考 附录 E.2。

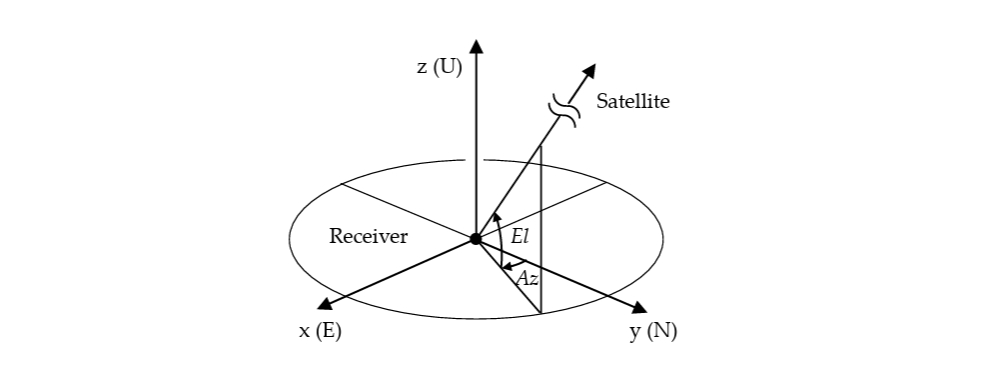
图E.3-4 局部坐标系与方位角和仰角