4. EKF

EKF单点定位的核心是将伪距、载波相位或多普勒观测值作为输入，通过非线性状态空间模型描述接收机运动状态和观测关系，利用EKF对状态进行最优估计。EKF通过线性化非线性观测方程，结合系统噪声和观测噪声的统计特性，递归更新状态估计和协方差矩阵。

4.1 基于EKF的观测域滤波

4.1.1 时间更新

状态以及其相应方差协方差的预测在以下函数中实现：

/* temporal update of position/velocity/acceleration */
static void UdposSPP(rtk_t *rtk, sol_t *sol_lsq, double tt)

这里实现的是PVA模型，也即位置/速度/加速度模型。函数的输入tt是相邻两次状态转移的时间间隔，主要是过程噪声的计算需要依赖tt。直观上也很容易理解，外推时间越长，过程噪声设置应该越大。

1. F阵的构建

for ( i = 0 ; i < 6 ; i++ ) {
    F [ i + ( i + 3 ) * nx ] = tt;
}

速度相关项的设置如上若是。这个循环设置了速度到位置的状态转移关系，将F矩阵中位置与速度相关的元素设置为时间间隔tt。

for ( i = 0 ; i < 3 ; i++ ) {
    F [ i + ( i + 6 ) * nx ] = SQR ( tt ) / 2.0 ;
}

加速度相关项的设置如上所示。这个循环设置了加速度到位置的状态转移关系，使用时间间隔tt的平方除以2来计算加速度对位置的影响。

2. Q阵的构建

/* process noise added to only acceleration */
 Q[0] = Q[4] = SQR(rtk->opt.prn[3]) * fabs(tt);
 Q[8] = SQR(rtk->opt.prn[4]) * fabs(tt);
 ecef2pos(rtk->x_spp, pos);
 covecef(pos, Q, Qv);
 for (i = 0; i < 3; i++) {
    for (j = 0; j < 3; j++) {
        rtk->P_spp[i + 6 + (j + 6) * NX_F] += Qv[i + j * 3];
    }
 }

RTKLIB中的Q只对加速度噪声进行了定义。在时间更新时，P和Q可以看作一个整体，而加速度的噪声，总会通过PVA运动模型通过状态转移传递到位置与速度项中。

3. 钟噪声的处理

/* add the receiver clk process noise */
for (i = 9; i < NX_F;i++) {
    rtk->P_spp[i + i * NX_F] += SQR(10000);
}

这里给钟增加了非常大的噪声，因此每次钟都会重新估计。

4.1.2 量测更新

1. 滤波中残差的描述

rescode和ResdopFilter分别构建了残差项v和设计矩阵H，而滤波的验前残差其实就是新息，为了记住其数学顺序，我们可以管这个过程叫OMC（Observation Minus Computation）。另外需要注意的是RTKLIB中的设计矩阵H实际是真实设计矩阵的转置。

Kalman滤波的残差计算和最小二乘的类似，最小二乘中计算的是基于概略位置的修正值，Kalman滤波也一样，也是相对于预测状态的更新量。区别在于Kalman滤波算法的状态量增加了速度和加速度。

2. rescode（伪距H和v的构建）

设计矩阵和残差阵依然采用最小二乘的rescode函数，只是将其中接收机所在位置进行了更新。

此前最小二乘的状态x只有位置和钟，但是现在增加了速度和加速度，因此增加了6个维度。

InsertVelAcc(nv, H);

为了方便，这里的rescode和原本基本保持了一致，内部暂时没有考虑速度和加速度。不过在rescode执行结束以后，在外层修改了H，从而增加速度和加速度项。另外v和var是向量，它们的维度仅与nv有关（有效观测的数目）。

3. ResdopFilter（多普勒H和v的构建）

/* range rate residuals */
static int ResdopFilter(const obsd_t *obs, const int n, const double *rs, 
const double *dts, const nav_t *nav, const double *rr, 
const prcopt_t *opt, const ssat_t *ssat, const double *x, 
const double *azel, const int *vsat, double *v, double *var, 
double *H)

构建速度观测项时，我创建了ResdopFilter函数，其本质上和原先的resdop相差不多，只是在一些状态位上存在一些差异。

在加权方面，原本的resdop使用了sig，这里主要是对不同频段的信号进行了简单的加权。速度的加权我使用了varerr，这部分代码原本是对伪距设计的，不过如果将其中的缩放因子进行合理调节，也能用于多普勒，这里参考3.2节。此前的x[3]项是钟漂，并认为所有系统的钟漂都是一样的。

4. 滤波

新增的Kalman滤波算法逻辑与RTK算法中完全一样。复用了filter函数，filter函数中调用了filter_，调用之前做了进一步处理，即仅状态值非0且方差大于0的状态参与滤波。这样处理是因为在RTK中默认的状态量包含了所有卫星的模糊度，对于没有观测值更新的模糊度明显是不需要参与滤波的。

所以在使用该filter时，注意各状态量的初值不要设置为0。或者直接调用filter_函数。将滤波结果更新回rtk_t->x_spp和rtk_t->P_spp中，便于下一历元的处理。同时将滤波存储到sol_t中。

4.1.3 检验代码的合理性

增加算法功能最麻烦的是，不确定自己所写的代码是否正确，尤其是遇到结果似是而非的时候，此时需要诊断“当前的情况究竟是错误还是误差”。这里我的解决方法是找到一个正确的开始，并基于这个初始的代码新增功能，确保功能增加后性能有所提升。

在完成EKF的代码后，一种“找到正确的开始”的方法是将EKF设置不相信预测，并充分相信观测中的伪距，然后看它的结果是否和单纯的最小二乘的结果一致。

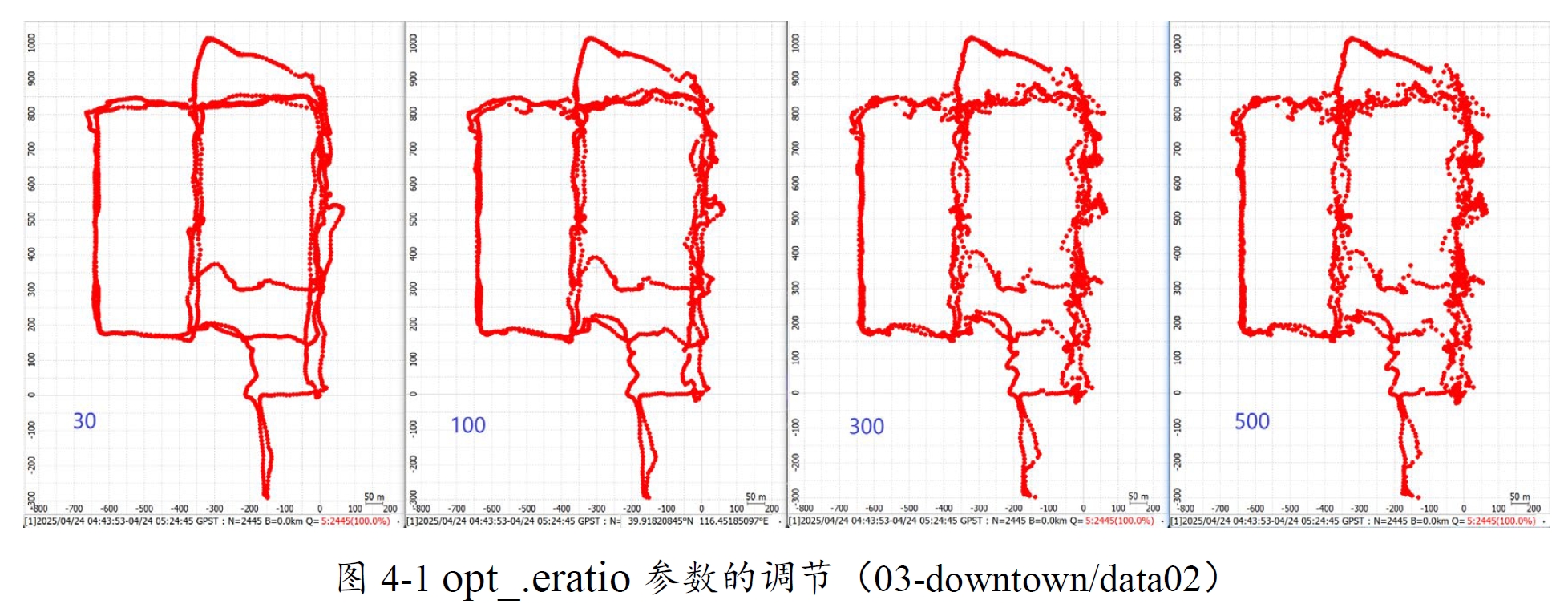
源码中使用rescode和ResdopFilter共同构建H和v阵，并最终用到量测更新中。在ResdopFilter中通过代码内部的opt_.eratio来控制最终伪距与多普勒之间的信赖关系（类似RTKLIB原本的stats-errdoppler），将其设置较大数值基本就和WLS的效果差不多了，通过这种方式可以检查自己的代码流程是否有问题，如图4-1所示。

EKF中的Q与R的比率决定了是信赖预测还是信赖观测，R内部针对伪距和多普勒的权重，决定了是信赖伪距还是信赖多普勒，而预测中主要使用的速度项由多普勒计算得到。

4.2 零速修正

if (fabs(enu[0]) < 0.5 && fabs(enu[1]) < 0.5 && norm(x_last,3) >= 1000) {
    rtk->nzupt++;
    rate = 1.0 / rtk->nzupt;
    if (rate == 1.0) {
        for (j = 0; j < 3; j++) {
            x[j] = x_last[j];
            x[j+3] = 1e-4; // [3:5]
        }
    } else {
        for (j = 0; j < 3; j++) {
            x[j] = x_last[j] * (1-rate) + x[j] * rate;
            x[j+3] = 1e-4; // [3:5]
        }
    }
} else {
    rtk->nzupt = 0;
}

上述代码是ZUPT（Zero Velocity Update, 零速修正）逻辑的核心部分，通过坐标转换和条件判断实现零速检测，并在检测到静止状态时更新状态向量，融合历史和当前数据以提高定位精度。注意在检测零速前，需要将速度量从ECEF坐标系转到ENU坐标系下。

ZUPT：当检测到ENU坐标系下水平速度（东向和北向）偏移量较小（<0.5米）且位置远离原点时，则假设系统处于静止状态（零速度），通过ZUPT来校正状态向量，减小漂移误差。

平滑融合：通过rate因子，代码在多次ZUPT中逐步减小当前状态的权重，更多依赖历史状态（x_last），从而实现平滑的位置和速度更新。

4.3 自适应Q

stat = pntpos(obs, n, nav, &rtk->opt, &sol_lsq, azel, rtk->ssat, msg);
UdposSPP(rtk, &sol_lsq, dt);
 
if (stat > SOLQ_NONE) {
    double y[6] = {0};
    double yi[6*6] = {0};
 
    for (i = 0; i < 6; i++) {
        y[i] = sol->rr[i] - sol_lsq.rr[i];
    }
    matmul("NT", 6, 6, 1, y, y, yi);
 
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 3; j++) {
            // set velocity residual to P_spp
            rtk->P_spp[(i+3) + (j+3) * NX_F] += yi[(i+3) + (j+3) * 6];
        }
    }
}

我使用了EKF预测的速度与RWLS的速度差值来构建Q中的速度协方差项，这是一个我偶然发现的谈不上专业的方法，但是它是有效的，因此我保留了这部分代码。

一些利用残差进行自适应Q调节的方法可能会用到滑窗的技术[08]，不过目前暂未对其进行尝试。

4.4 EKF中使用RWLS

4.4.1 EKF中的抗差

在使用最小二乘进行单点定位时，抗差和定位共用了同一个LSQ。但是EKF中，没有可共用的LSQ。这里需要以位置和速度项联立构建一个新的最小二乘表达式，并求得新的v与H，然后将其提供给EKF量测更新。

for (j = 0; j < nv; j++) {
    for (k = 0; k < NX_F-3; k++) {
        if (k >= 6) {
            H_new[k + j * (NX_F-3)] = H[k+3 + j * NX_F];
        } else {
            H_new[k + j * (NX_F-3)] = H[k + j * NX_F];
        }
    }
}

具体的，构建H和v矩阵需要去除加速度项，因为H阵的加速度项全为0，这样会导致H阵不可逆，导致最小二乘解算失败，其去除过程如上所示。至于剩下的部分则与第3章相同。

4.4.2 伪距残差的零均值问题

1. 伪距残差水平

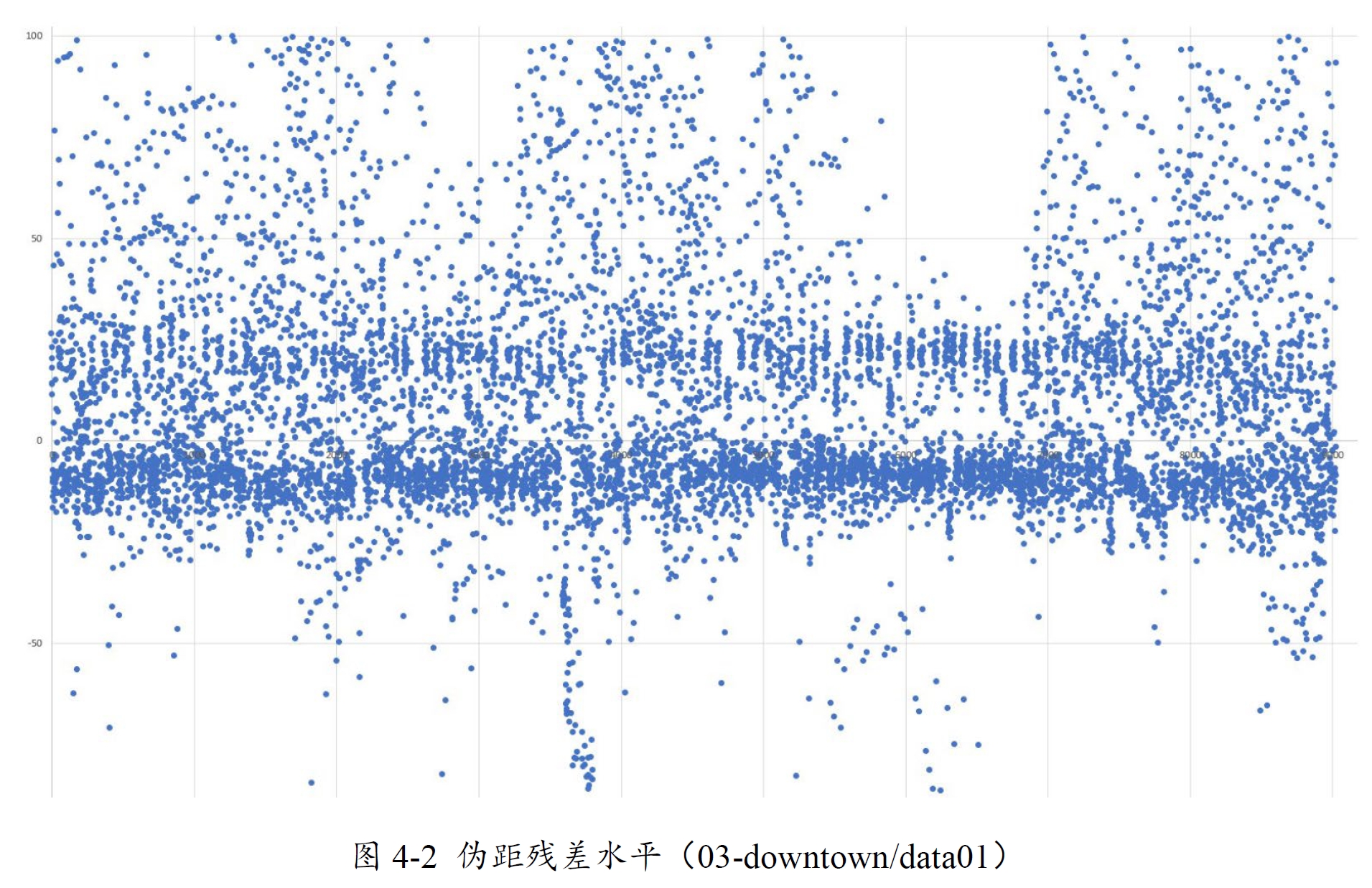
上图是手机伪距的验前残差（截取±100之间数值），发现：

正值的落点比较稀疏，负值的落点相对密集；
同时正值相对密集区域的均值（大概+20左右）比起负值密集区域的均值（-10左右）绝对值较大。

整体上伪距残差并没有符合零均值分布的特点，存在一定的正偏。

2. 残差与SNR

根据SNR加权模型可计算出一个伪距误差项，残差应该和SNR误差项是相关的，直接使用残差除以SNR标准差（正值）得到如下情况（类似标准化）。

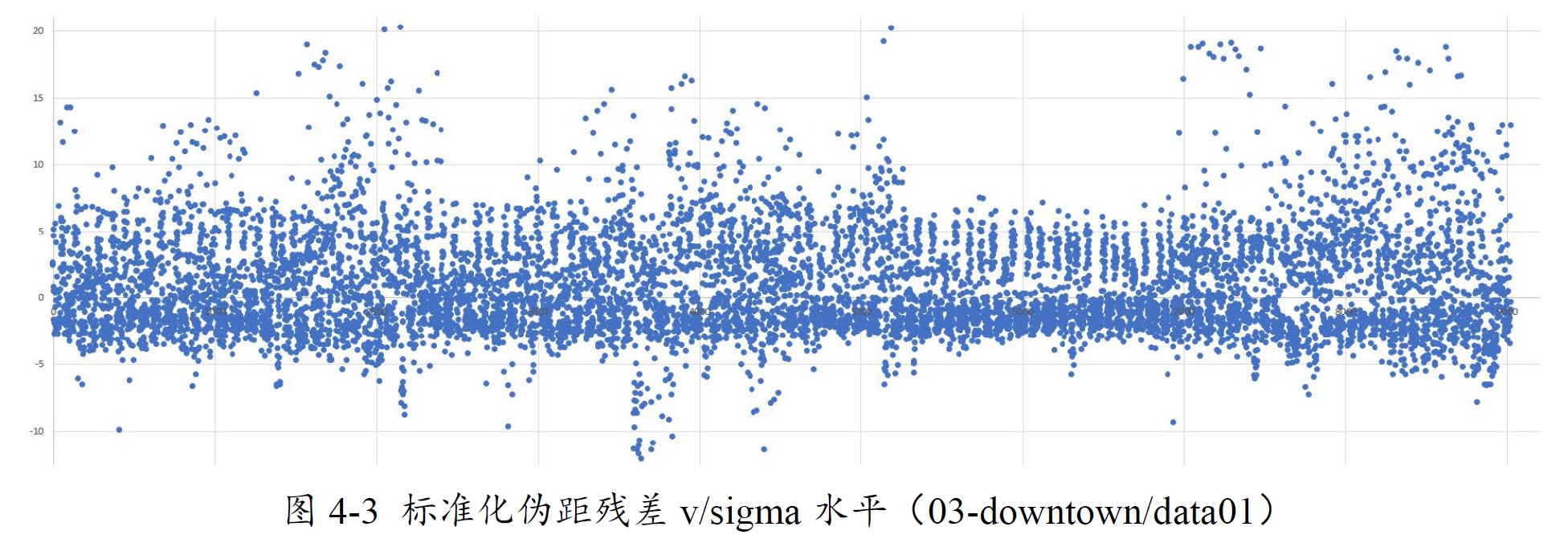
上述操作类似标准化，让残差的水平更加集中，从而方便观测，上图同样是不满足零均值的，如果将其进行零均值修复，发现对结果有极大的改善。这里的N来自上图的均值偏差（约2.5），sigma是SNR加权模型计算得到的标准差。

// RobustFilter外部
for (j = 0; j < nc; j++) {
    v[j] -= 2.5 * sqrt(var[j]);
}
RobustFilter(H_new, v, NX_F-3, nc, nd, NULL, var);
 …
// RobustFilter内部
for (i = 0; i < nc; i++) {
    v_new[i] -= 1.0; // v_new已经归一化
}

零均值修复既可以放在抗差前，也可以放在抗差的过程中，不过似乎放在抗差的过程中效果会更好一些。至于为什么这么做能够提升算法性能，猜测是因为残差符合零均值分布会让抗差更均匀，从而提高了最终性能。

4. EKF ​

4.1 基于EKF的观测域滤波 ​

4.1.1 时间更新 ​

4.1.2 量测更新 ​

4.1.3 检验代码的合理性 ​

4.2 零速修正 ​

4.3 自适应Q ​

4.4 EKF中使用RWLS ​

4.4.1 EKF中的抗差 ​

4.4.2 伪距残差的零均值问题 ​

4.4.3 抗差EKF性能 ​