2. 数据分析
算法调试前的数据分析是一项很容易被忽视的工作,可能很多人为了省事,喜欢直接将算法先跑起来,然后再进行一系列修改。我认为对于需要优化的对象保持一个更全面的认识总归是不会错的。
MobileGNSS-SPP主要针对客户提供的某一款GNSS芯片进行了优化(其型号暂时无从得知),该芯片数据是L1单频的,不过它提供了多星座支持(GPS、BDS、GLO、GAL、QZS)。本章节还会对其中一些具体的数据指标进行分析。
2.1 数据采集
2.1.1 测试平台
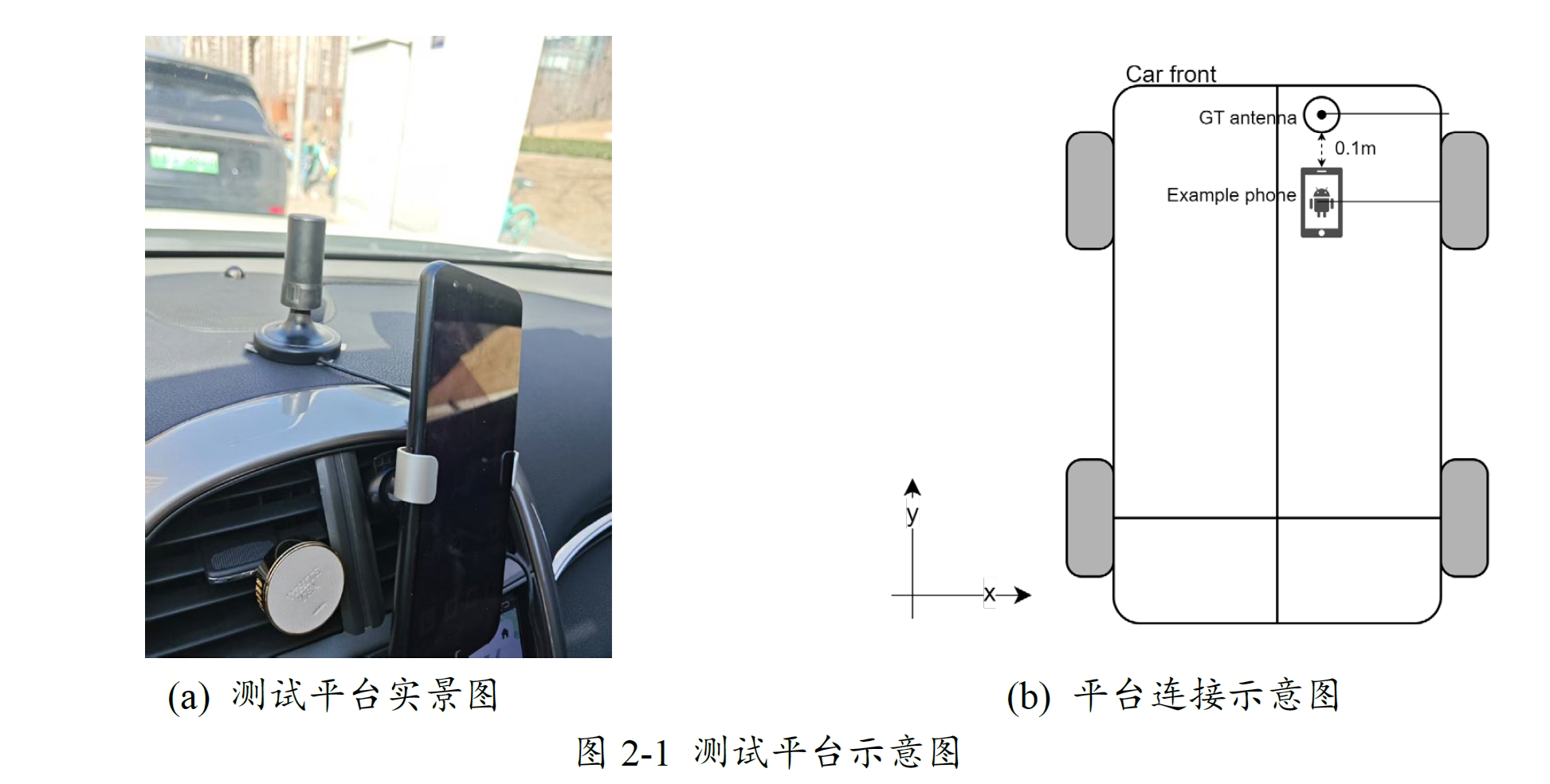
测试平台如上所示,测试设备为目标安卓手机、和芯星通UM982(RTK),测试软件为GEO++、GNSSLogger。数据分析和后续算法的提升都是基于上述平台所录制的数据进行的。
经过实测发现GEO++录制的数据更完整,GNSSLogger录制的数据中某些卫星经常会缺失伪距观测数据,不过GEO++偶尔也会异常,导致中间记录中断,并缺失较长一段时间的数据。整体上原始数据的录制还是以GEO++为主,异常的时候就多录制几组,而GNSSLogger用来记录原厂算法的结果(NMEA)作为基准结果进行对比参考。
至于星历数据的采集方式参考附录A.2。
2.1.2 测试场景
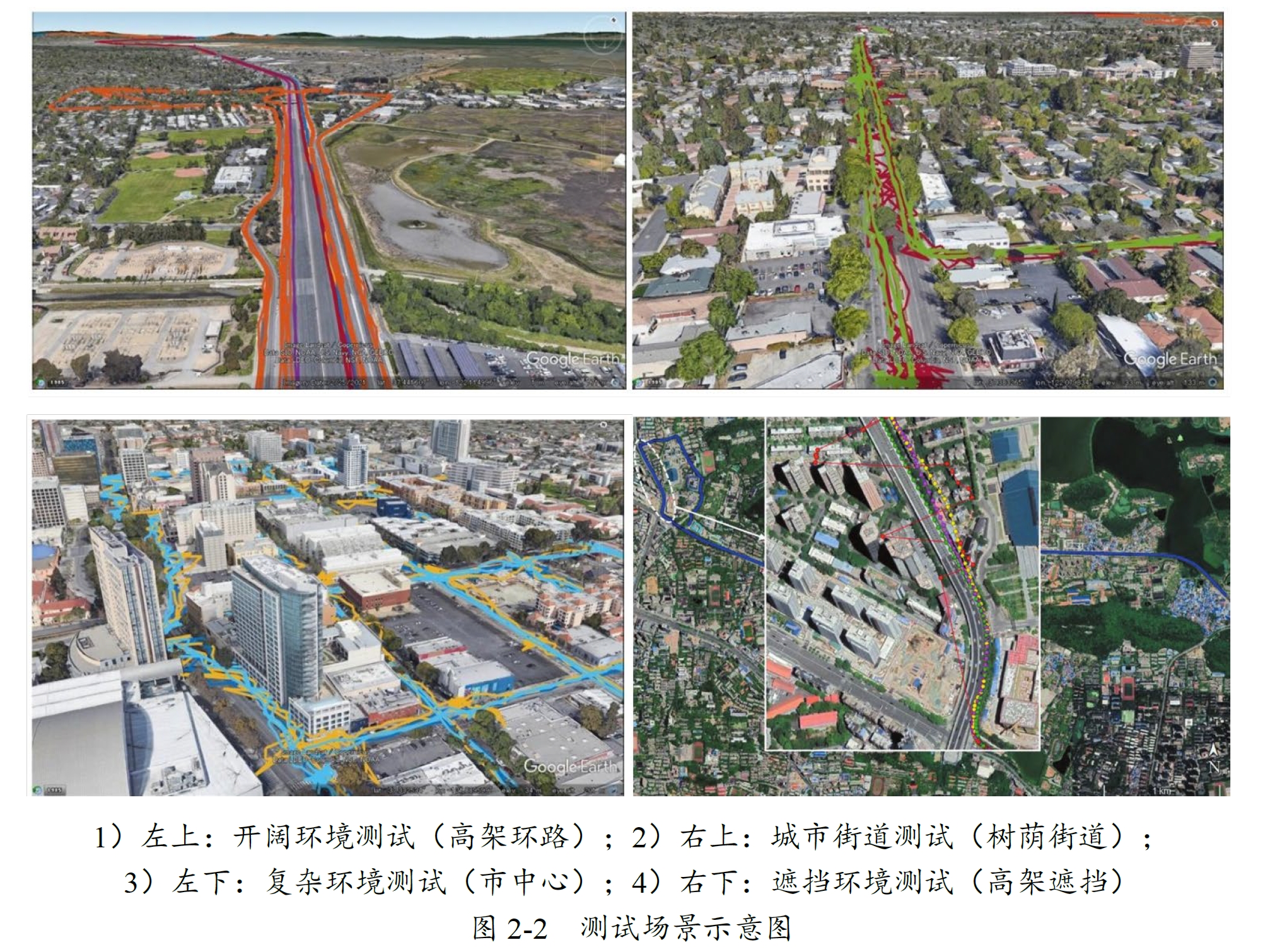
测试场景分类:
| 测试场景 | 描述 |
|---|---|
| 开阔环境(高速公路) | 在高架桥面、城市外环路等开阔直线路段测试,GNSS 信号接收条件优越,适合评估高速移动和无障碍环境下的性能。 |
| 城市街道(树荫遮挡) | 在有路边树木的城市街道测试,存在一定程度的 GNSS 信号遮挡,评估部分干扰下的性能。 |
| 复杂城市环境(市中心) | 在高楼林立、建筑密集的市中心测试,GNSS 信号受多路径和遮挡干扰,挑战系统鲁棒性。 |
| 遮挡环境(高架桥下) | 在高架桥下或附近测试,桥墩、桥面及周边建筑导致信号遮挡和反射,形成复杂信号环境。 |
2.2 C/N0(载波噪声密度比)
C/N0(dB-Hz)是GNSS领域中最标准的信号质量指标。但是由于叫法上的习惯,大家也会称作SNR(信噪比),其具体区别参考附录A.1。
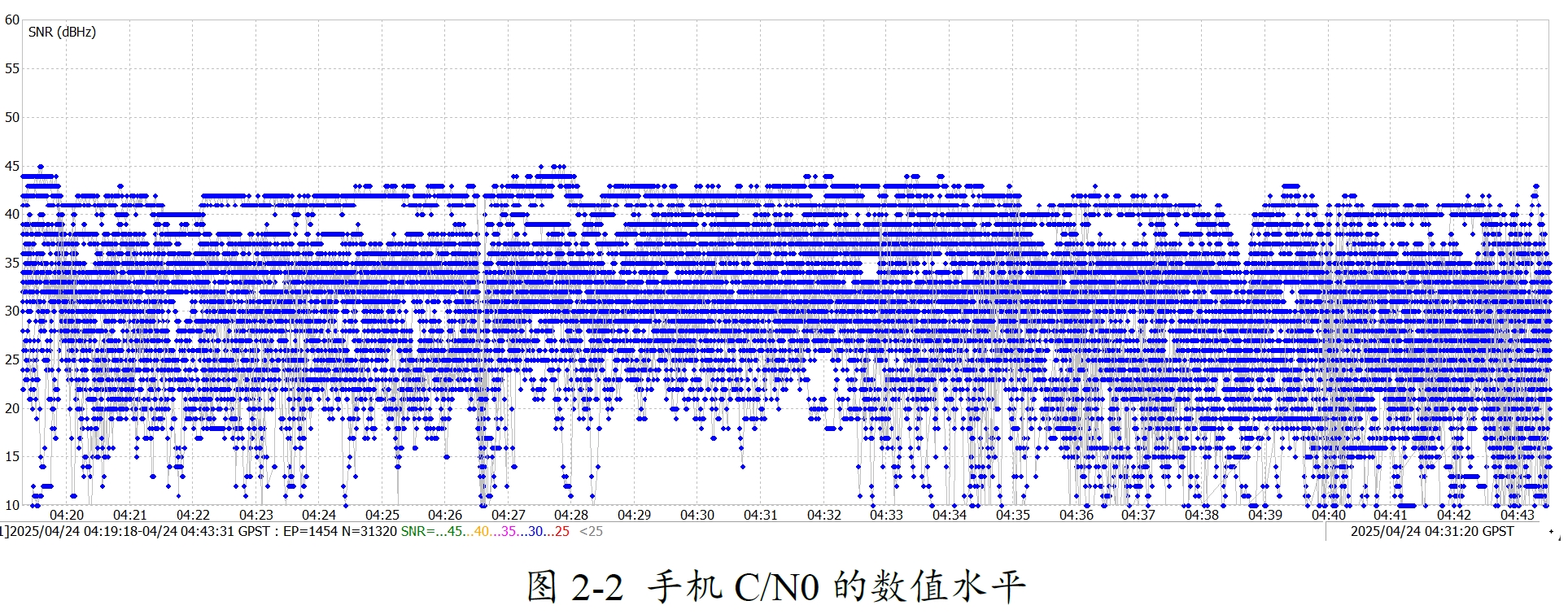
由开阔数据的表现来看,C/N0最大在45左右,相应的RTKLIB配置stats-snrmax需要设置为45,而C/N0的截断阈值pos1-snrmask则需要设置为10,尤其针对高架遮挡场景,如果设置较高,会导致很多历元卫星数目不够。而设置为10时,如果抗差逻辑表现良好,并不会让算法在其他场景下表现更差。
配置文件位于MobileGNSS-SPP\app\rnx2rtkp\conf。
2.3 观测间的相关性
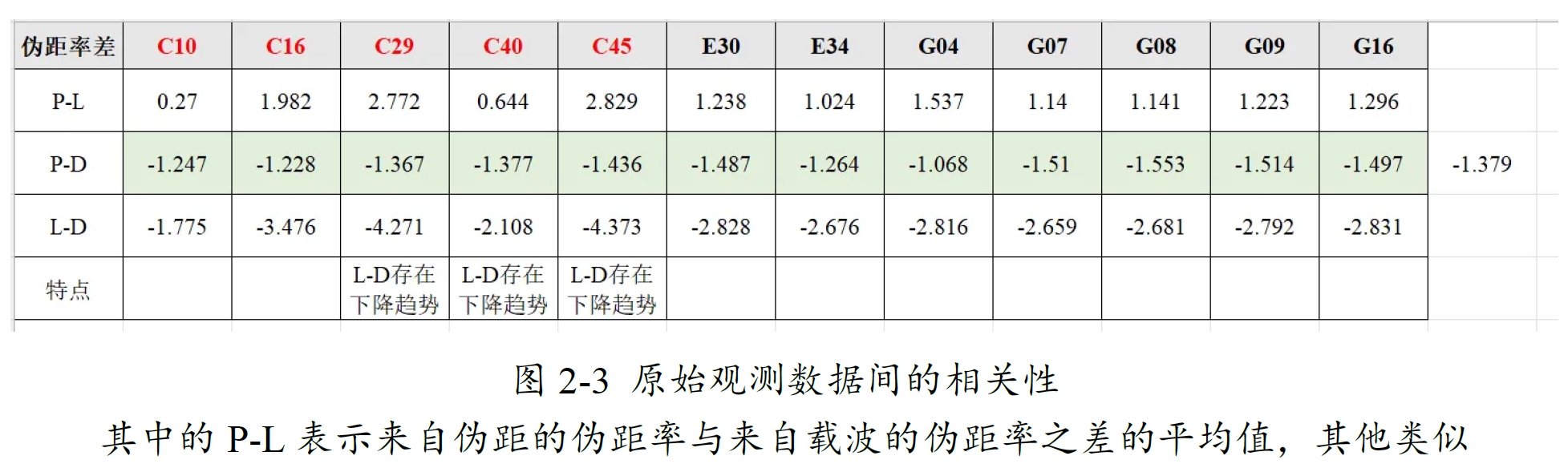
参考GSDC(2023-2024)第二名参赛选手Suzuki的分析[01],可以通过计算来自不同物理量的伪距率,并两两相减,从而判断物理量之间的相关性(差值为0则相关,不为0则不相关)。
通俗来理解,伪距率即代表了卫星与接收机间的相对速度,这个相对速度除了通过多普勒计算得到,也可以通过伪距或载波在单位时间上的距离变化得到。速度相较于距离的变化会更慢一些,通过对伪距率的研究发现:
- 该芯片物理量中的观测量两两不匹配;
- 伪距和多普勒之间的关系相对其他关系更为稳定(平均在-1.379左右),不过暂时没有发现其背后所代表的含义;
- 北斗的载波测量非常不稳定,系统误差比较大。
至于判断是否相关之后又能做什么,这里参考Suzuki的做法。
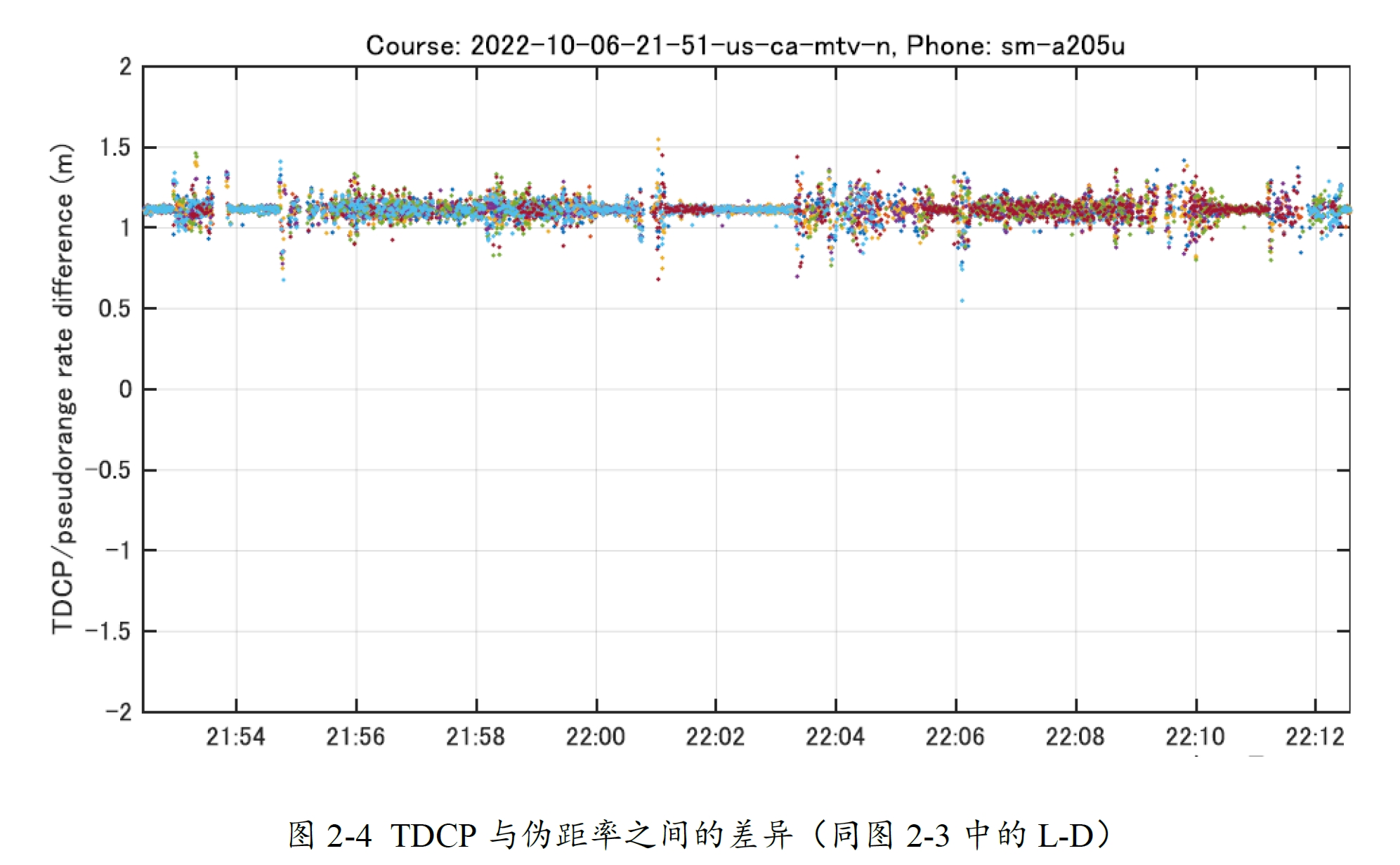
图2-4为Suzuki计算的TDCP与伪距率之间的差值(L-D)。通常,这种差异应为零。然而图2-4显示某些智能手机的TDCP中包含大约1.1米的固定偏差误差。对于这些手机,需要预先校正其偏差误差,并将其用作于TDCP因子。

通过查看Suzuki的代码[02],发现他直接将固定偏差补偿到TDCP上了,并认为多普勒数据是正确的。由于我们的数据中物理量之间两两不相关,所以并不知道哪个物理量是完全正确的。
2.4 伪距和多普勒之间的相关性
根据Suzuki论文中的介绍,伪距和多普勒相关性的比较主要看:利用伪距钟差算出的钟漂和利用多普勒算出的钟漂之间的相关性。不过我认为此前在2.3节中的分析也能判断出伪距与多普勒之间的相关性,图2-3中的P-D显示两者存在一个相对稳定的偏差(平均在-1.379左右)。
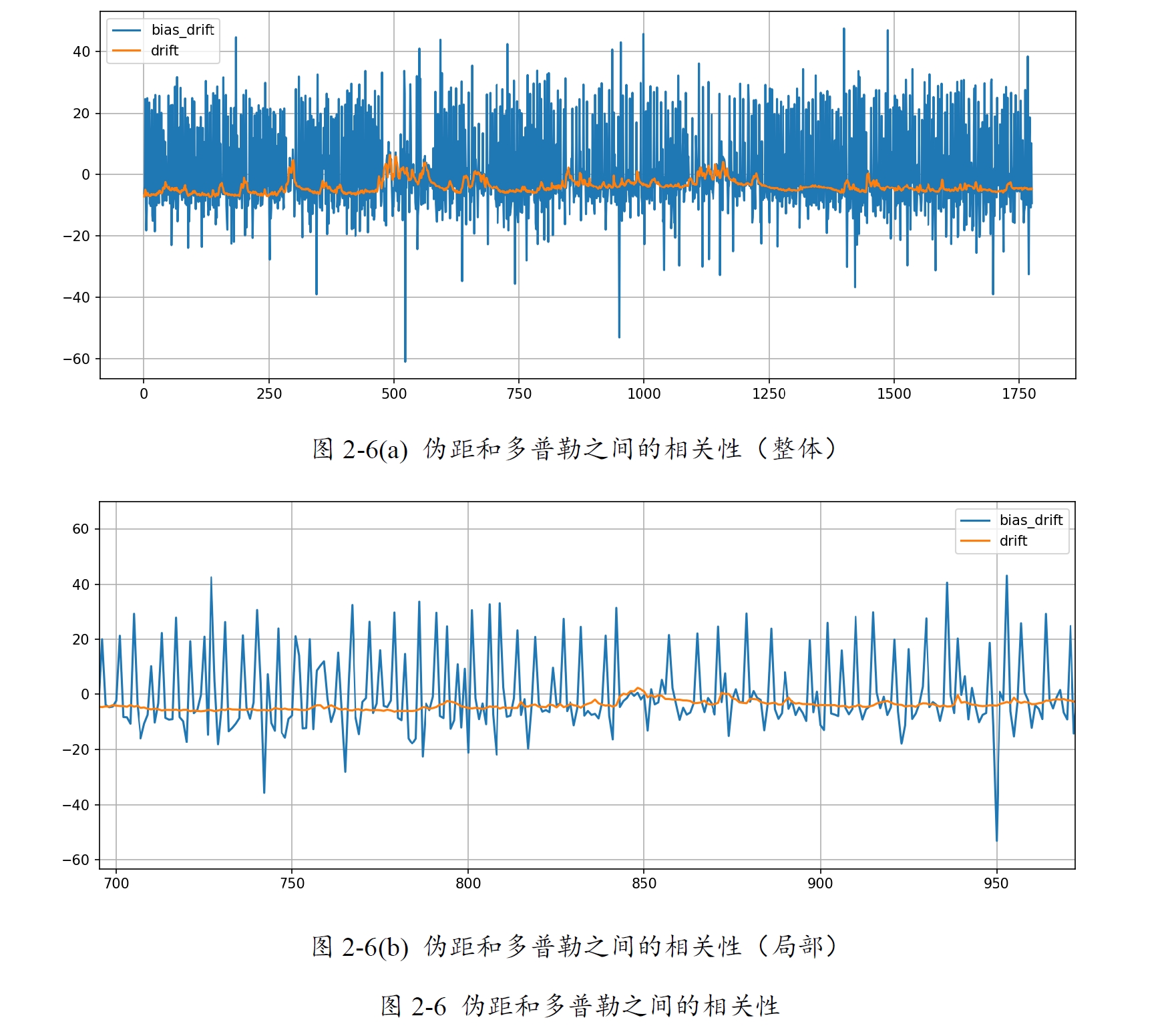
按照Suzuki的方法,从钟漂的角度来看伪距与多普勒之间的相关性。从2-6(a)发现,两种钟漂似乎中心并没有在一起;不过由2-6(b)发现,钟差里面吸纳了很多不规则的系统误差,它可能间隔一些历元出现,导致图中出现了很多毛刺(可参考2.5.2节中的分析)。如果去掉这些毛刺的话,似乎两者的中心线还是比较接近的。
由于我相信2.3节中P-D的结论,因此我暂且认为伪距与多普勒不相关,那么给我的启示是:在EKF估计器里,不要用钟漂递推钟差。
2.5 TDCP(历元间差分载波相位)
2.5.1 TDCP原理
在RINEX原始观测数据的语境下,ADR代表的就是载波相位。GSDC赛事中,高分选手几乎都用到了ADR,并用其进行速度估计。

多普勒和ADR都可以用来估计速度,而基于ADR计算的速度TDCP(来自载波的伪距率)比基于多普勒计算的速度更加精确(如图2-7所示)。基于ADR的伪距率TDCP计算如下:
TDCP的优点是可以实现相对开阔地段的亚米级定位。但是TDCP的准确性低于多普勒(因为需要考虑周跳和半周模糊度问题)。特别的,ADR的缺失通常发生在突然加速和减速中,此时的速度状态也会出现缺失[3]。
2.5.2 观测数据中的钟跳
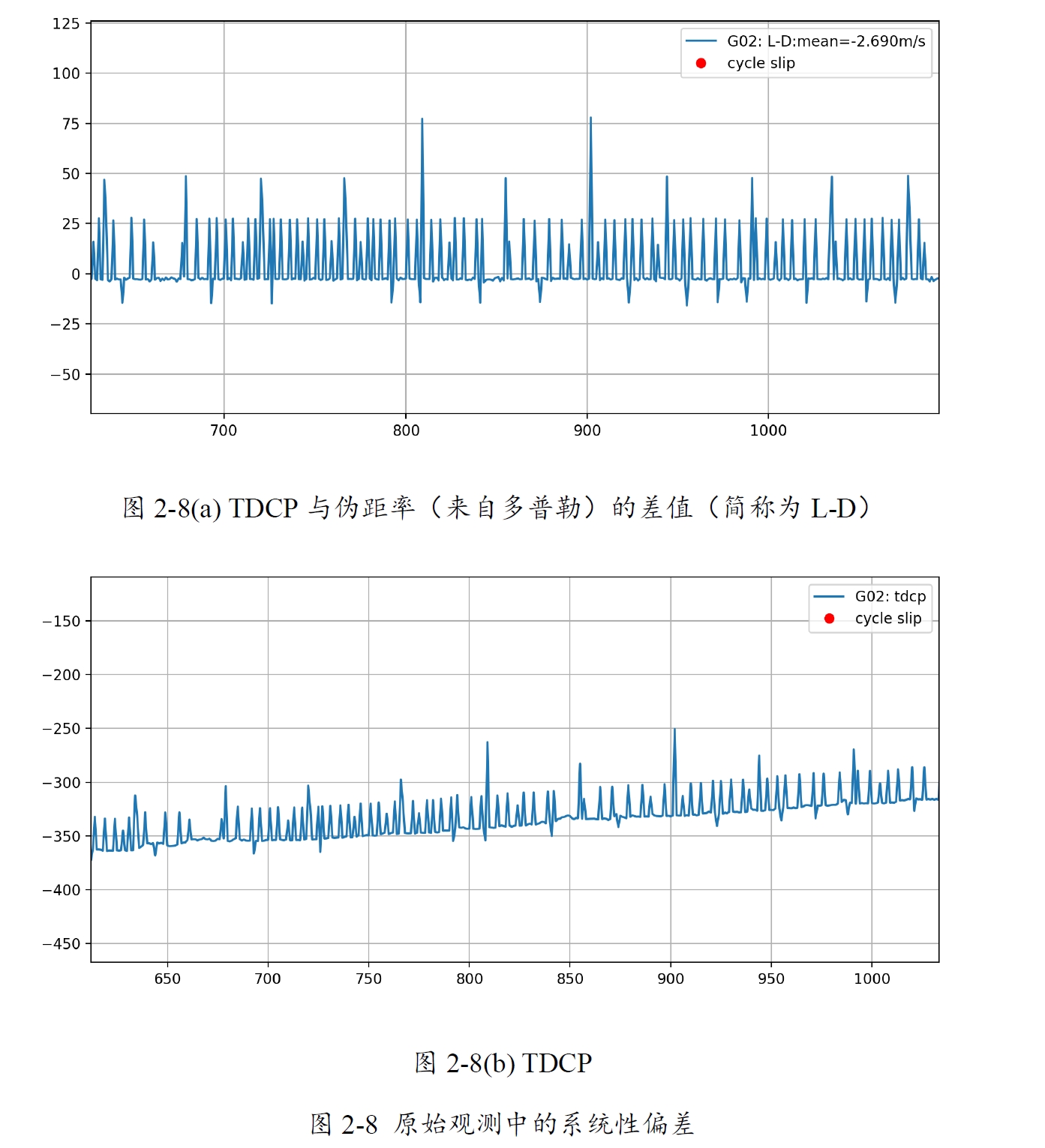
分析载波相位数据时发现,载波观测中存在一定的系统性偏差,它导致了TDCP和L-D数值中出现了很多毛刺,后续的研究发现,伪距中也存在相同的现象,并且某个历元出现问题,那么所有卫星都会存在该现象,而非某颗卫星独有。我暂时将其归因于钟跳,尽管通常不会每几秒就发生一次钟跳。
设备产生钟跳时,该误差通常会归到钟差项中,因此理论上它不会影响算法的运算结果,不过由于残差的变化,它可能会影响到后续残差相关的操作,由于我抗差会使用迭代最小二乘,而迭代过程中会消除钟差(含钟跳)的影响,因此钟跳将不会影响到后续的抗差部分。
