3. RWLS

由于最小二乘较为简单，能比较方便和快速地对一些方法进行验证，因此初始时我将利用最小二乘进行一些基础的优化。

3.1 加权模型

3.1.1 RTKLIB中的BUG

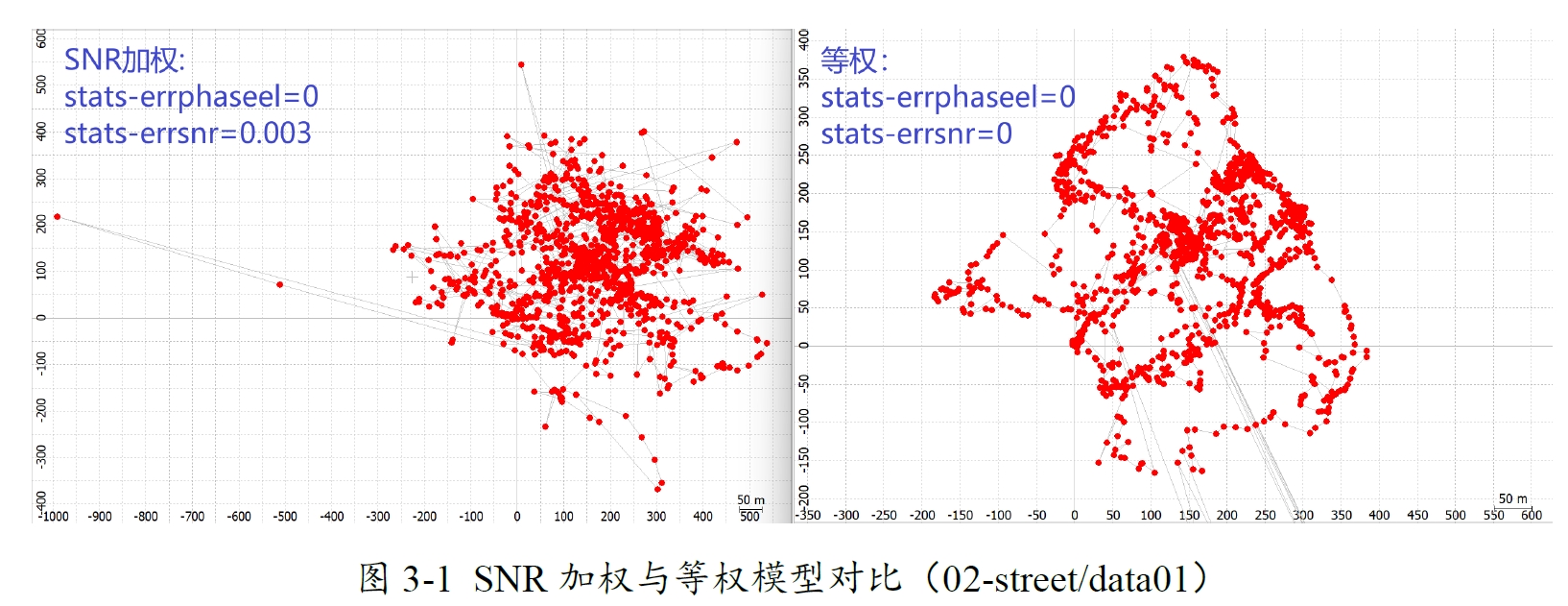
demo5-b34k版本的RTKLIB在打开SNR加权后轨迹会崩溃，不过这并不是因为SNR加权效果不如等权，这里显然是错误，而非误差。

将ssat[i]改成ssat[sat-1]即可解决，打开SNR加权将提升定位性能。

3.1.2 仰角与SNR加权

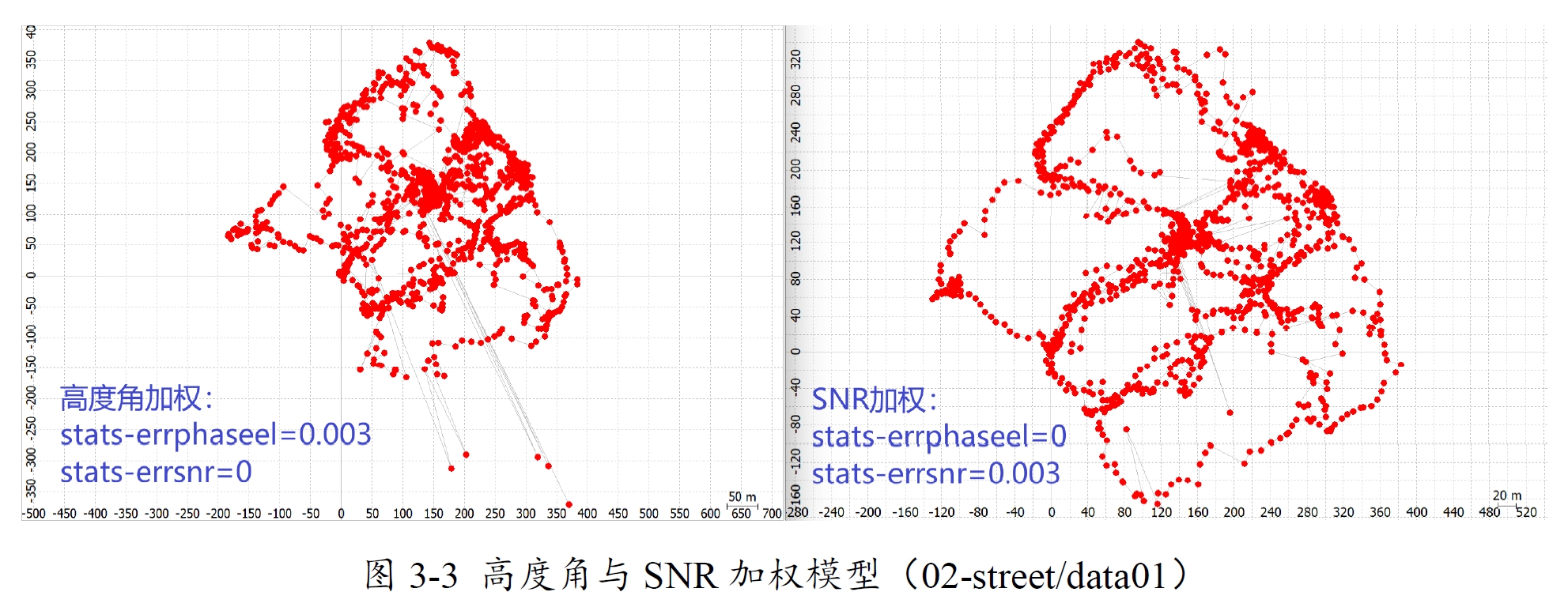
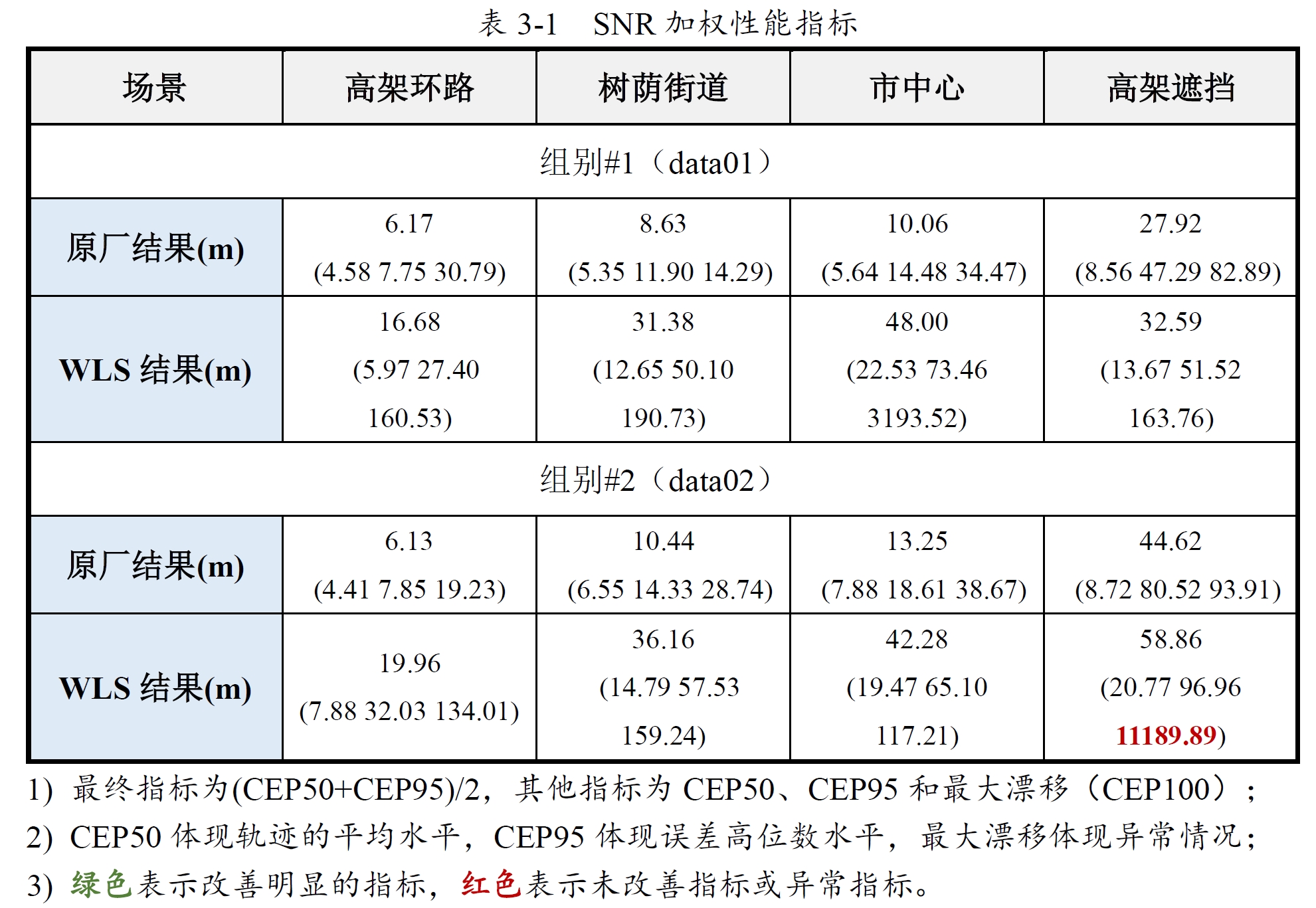
以上为使用SNR加权模型WLS在不同场景上的表现，目前由于代码中没有抗差，因此最大漂移指标都比较大。

基于卫星仰角的GNSS观测模型更适用于专用接收机。然而，对于智能手机，基于信号强度（载噪比，C/N0）的模型比依赖仰角的模型更能有效地处理观测权重[4,5,6]。因为智能手机观测误差往往由信号质量问题主导，而非大气误差，而使用仰角加权观测的动机正是为了解决大气误差

3.2 速度估计中的加权

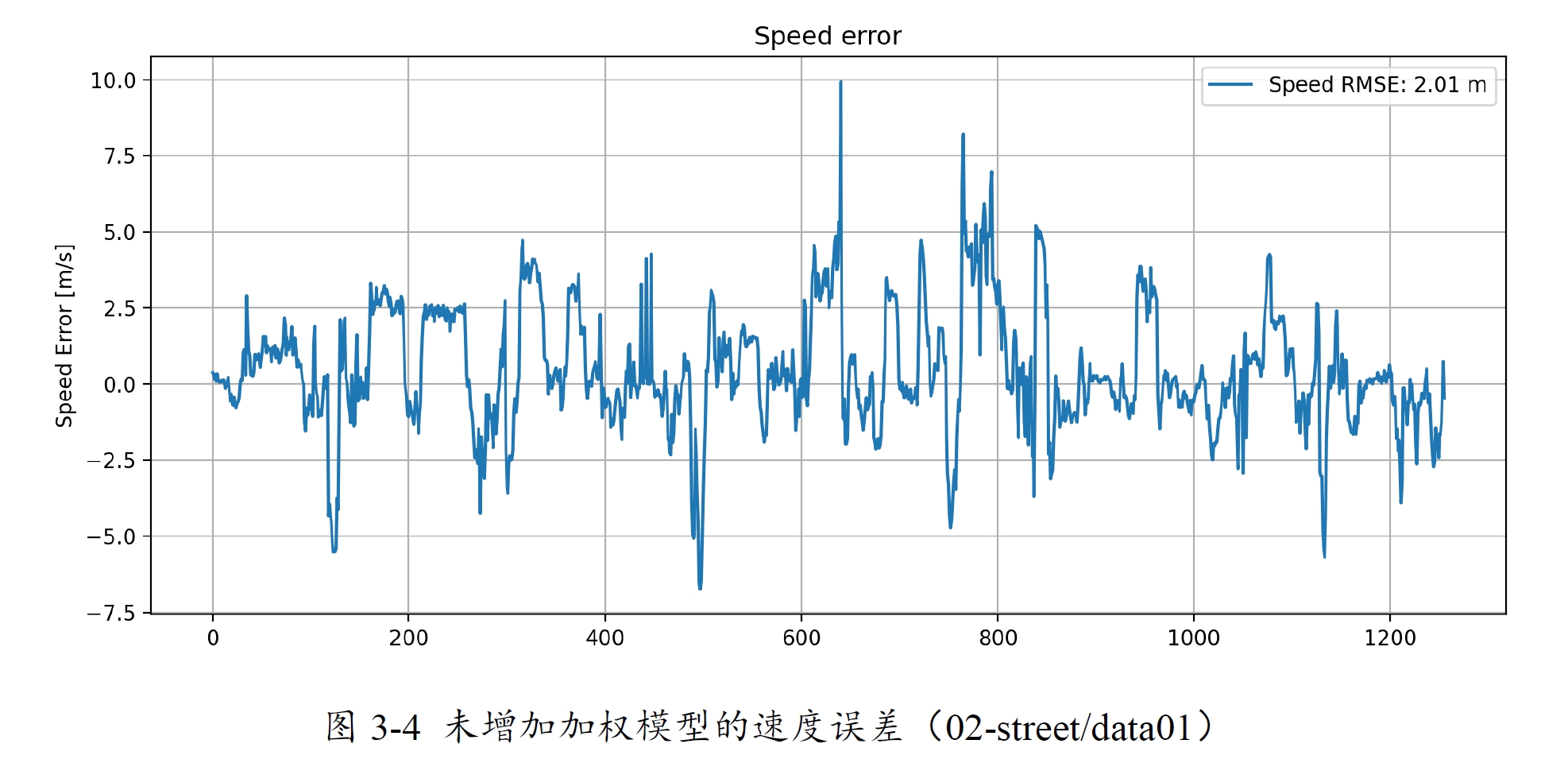
RTKLIB中的速度估计原本几乎没有进行加权，其表现的性能如图3-4所示，基本和等权差不多。

sig = (err <= 0.0) ? 1.0 : err * CLIGHT / freq;
var[nv] = SQR(sig);

原本加权方法的代码如上所示，其中的err由stats-errdoppler参数来控制。我在resdop中增加了新的加权方法，这里可以直接将伪距中的加权方法拷贝过来，并将原本的加权代码注释掉。

// resdop内部
prcopt_t opt_ = {0};
memcpy(&opt_, opt, sizeof(prcopt_t));
…
opt_.eratio[0] = 30.0; // doppler/phase error ratio
if (ssat)
    var[nv]=varerr(&opt_,&ssat[obs[i].sat-1],&obs[i],azel[1+i*2],sys);
else
    var[nv]=varerr(&opt_,NULL,&obs[i],azel[1+i*2],sys);
…
// 权的调节（修改H和v）
for (j=0;j<nv;j++) {
    sig=sqrt(var[j]);
    v[j]/=sig;
    for (k=0;k<4;k++) H[k+j*4]/=sig;
}

具体的，需要在resdop中增加var计算的代码，随后在resdop调用的地方进行加权操作。其中的opt_.eratio[0]表示stats-eratio1参数，它原本代表L1频点伪距误差相对于载波相位的缩放因子，因为varerr内部的模型是针对载波相位的。这里我拷贝了一份opt_，并以其中的opt_.eratio表示多普勒相对于载波相位的缩放因子，需要注意的是由于不再使用原本的加权方式，这就意味着stats-errdoppler参数将不再生效。

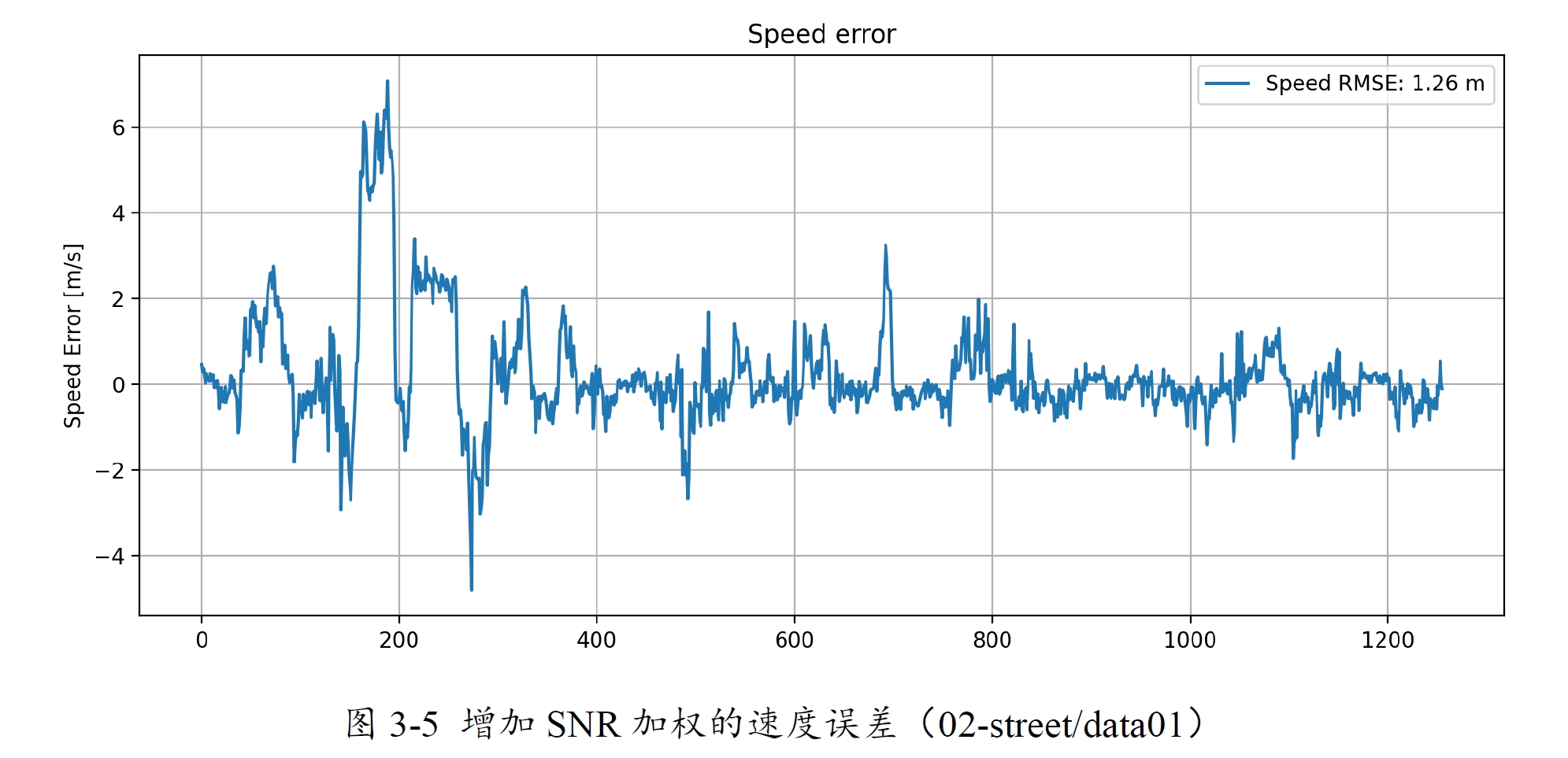
可以看到速度的误差水平有所降低。

3.3 M估计（抗差估计）

3.3.1 原理与实现

M估计是一种广义的最大似然估计方法，旨在最小化一个目标函数，该函数对异常值不敏感。其核心思想是通过定义一个损失函数（或称为目标函数）来替代最小二乘法中的平方损失。

如果换一个角度来看M估计，可以认为它是一种更可靠的加权模型，该加权模型还利用到了验前残差（或新息），验前残差反映了预测与观测之间的差距，差距越小则给观测更大的权重，反之则给观测更小的权重。

M估计的数学表达如上所示。M估计的损失函数（或目标函数）通常包括Huber、IGG3和Tukey模型等，这里我主要关注其中的Huber和IGG3模型。

static int RobustLsq(const double *H, const double *v, int nx, int nv, double *dx, double *Q, double *var, int mode)

以上为实现M估计的C语言代码，需要注意：

• 迭代流程。迭代最小二乘，先计算权，再更新H和v；
• dx初值。初始的时候需要将dx赋值为0，不然结果可能会出现毛刺，本质是增加了迭代次数，以及位置首次迭代会除以残差本身。

3.3.2 调参经验

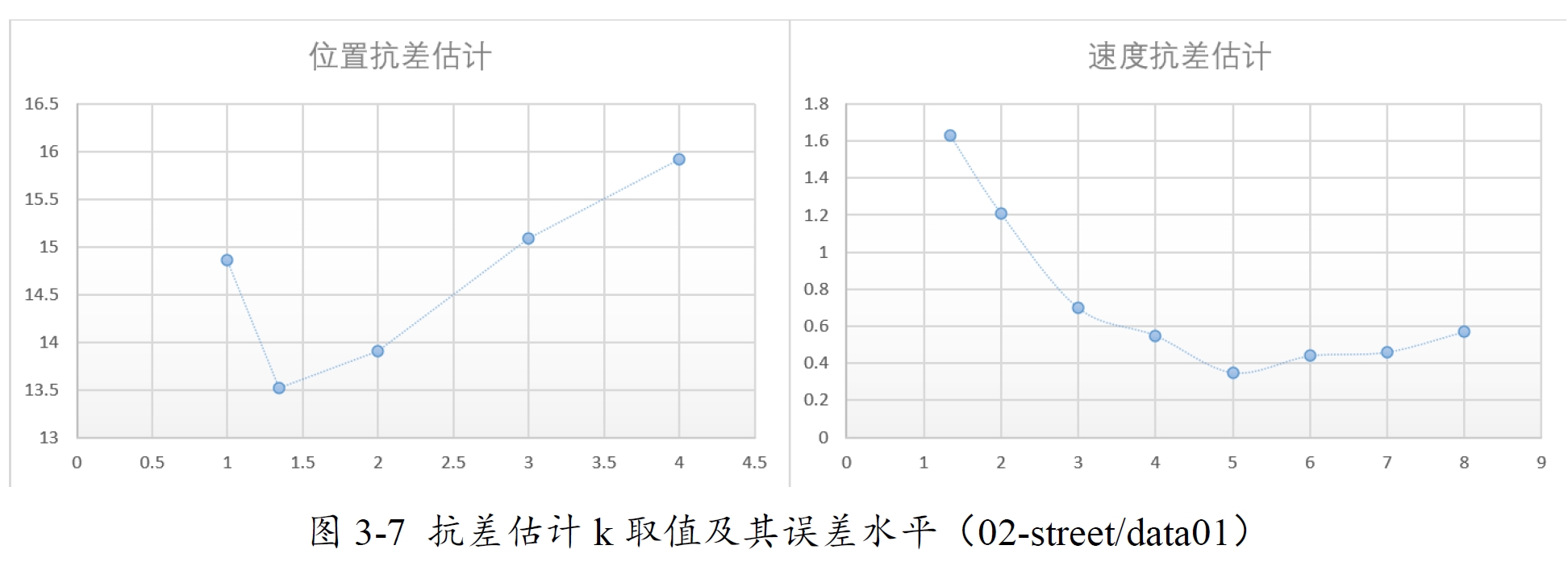
当前使用的Huber模型作为损失函数，位置抗差和速度抗差k的最佳取值是不同的，Huber模型中k默认为1.345，该取值对位置估计有效，但速度估计则需取值为5.0，k的取值更多的还是取决于测试数据所表现的残差水平，一般多试几次即可知道最佳取值。

当前场景中，IGG3模型没有很好用，尤其是IGG3的第三段，会导致一些残差较大但能正常运算的卫星失去作用，致使参与卫星过少，这主要是因为芯片中伪距中存在频繁的钟跳（参考2.5.2节）。

// 位置钟跳的粗略剔除
if (i == 0) AdjustClkJump(nv, H, x, v); /* median inner system as receiver clock */
 …
// 速度钟跳的粗略剔除
if (i == 0) {
    double med = DemianResOffset(v, nv, NULL, NULL);
    for (j=0; j<nv; j++) {
        v[j] -= med;
    }
    x[3] += med;
}

如果一定要使用IGG3模型的话，可以在使用前对所有残差数据扣除一个残差中位数（粗略代表钟跳），这样避免IGG3第三段操作时踢掉过多卫星；而Huber模型不需要扣除则是因为Huber不会剔除卫星，而迭代过程中则会消除钟跳误差。Huber等损失函数模型的实现请参考RobustWeightLsq，这里我是按照计算权值的方式对其进行定义的。

这里的Huber模型和IGG3模型的处理如下：

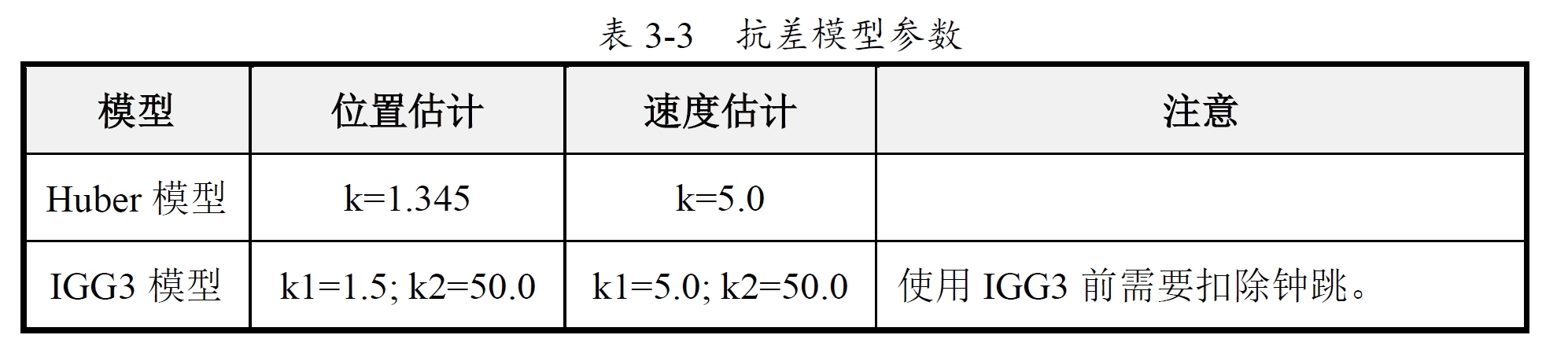
可以发现位置估计与速度估计时需要设置不同的参数，而IGG3模型由于面对的是整体残差较大的数据，因此k2需要设置得比一般情况更大的数值。

if ((mode==ROBUST_POS&&resid>=100) || (mode==ROBUST_VEL&&resid>=20)) {
    return 0.0001 / resid;
}

损失函数内部需要对残差较大的数据进行截断处理，即返回一个接近0的权值，另外不同算法的残差水平是不同的，需要设置不同的阈值（例如EKF中相应的部分需要设置为30、2）。

3.3.3 测试结果

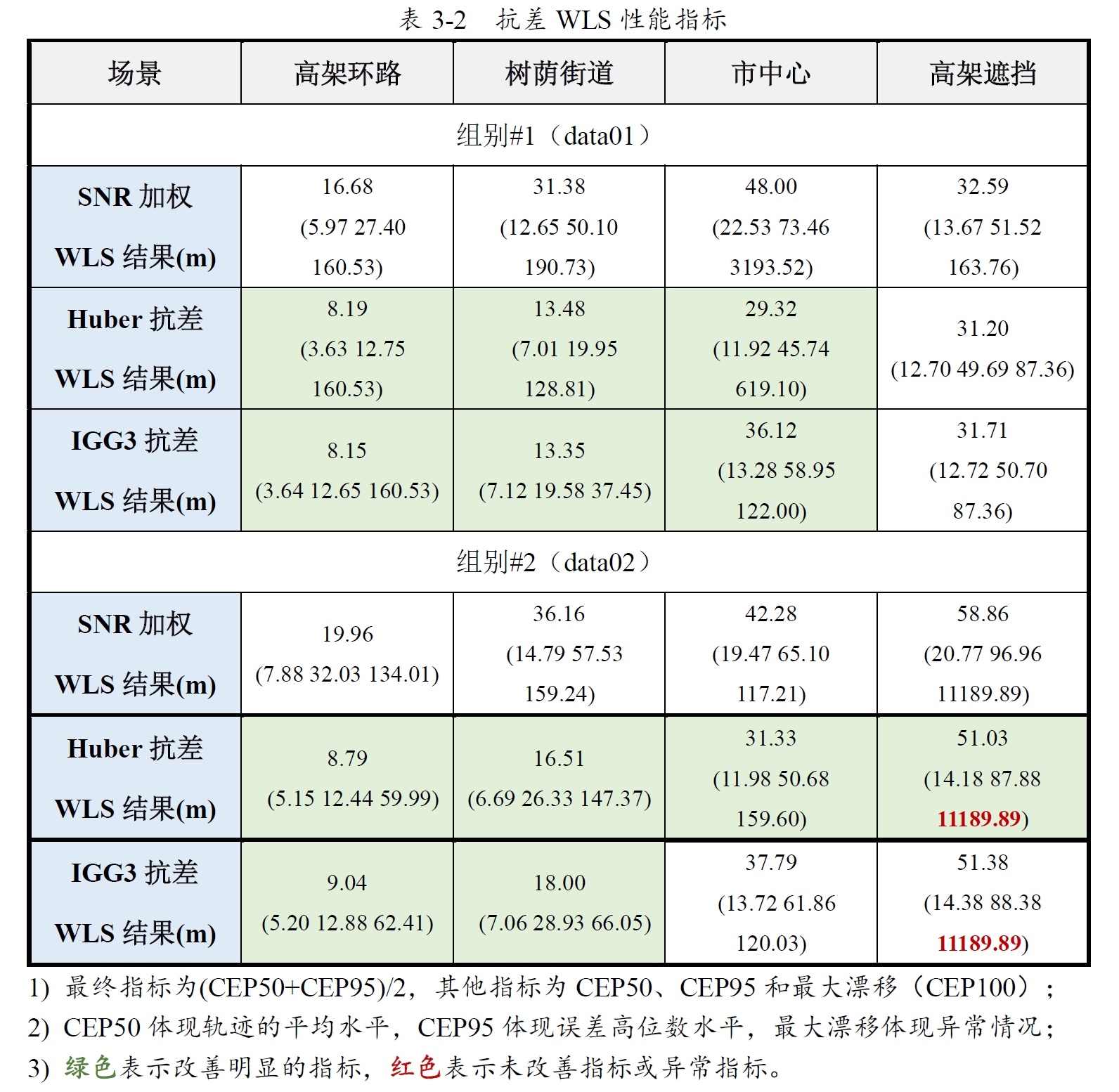
由上表可看到抗差最小二乘比单纯的SNR加权效果要很多。另外Huber的平均水平相较IGG3更好，而IGG3不会像Huber那样容易出现较大的异常偏差。

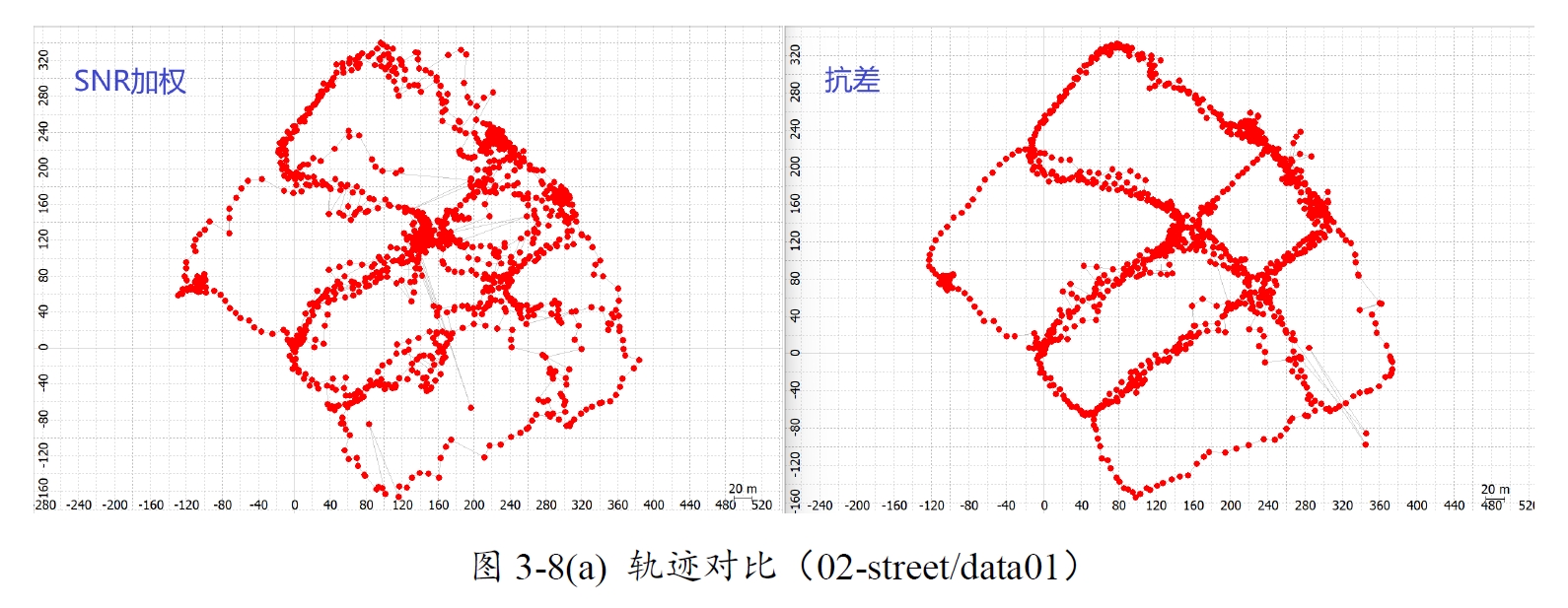
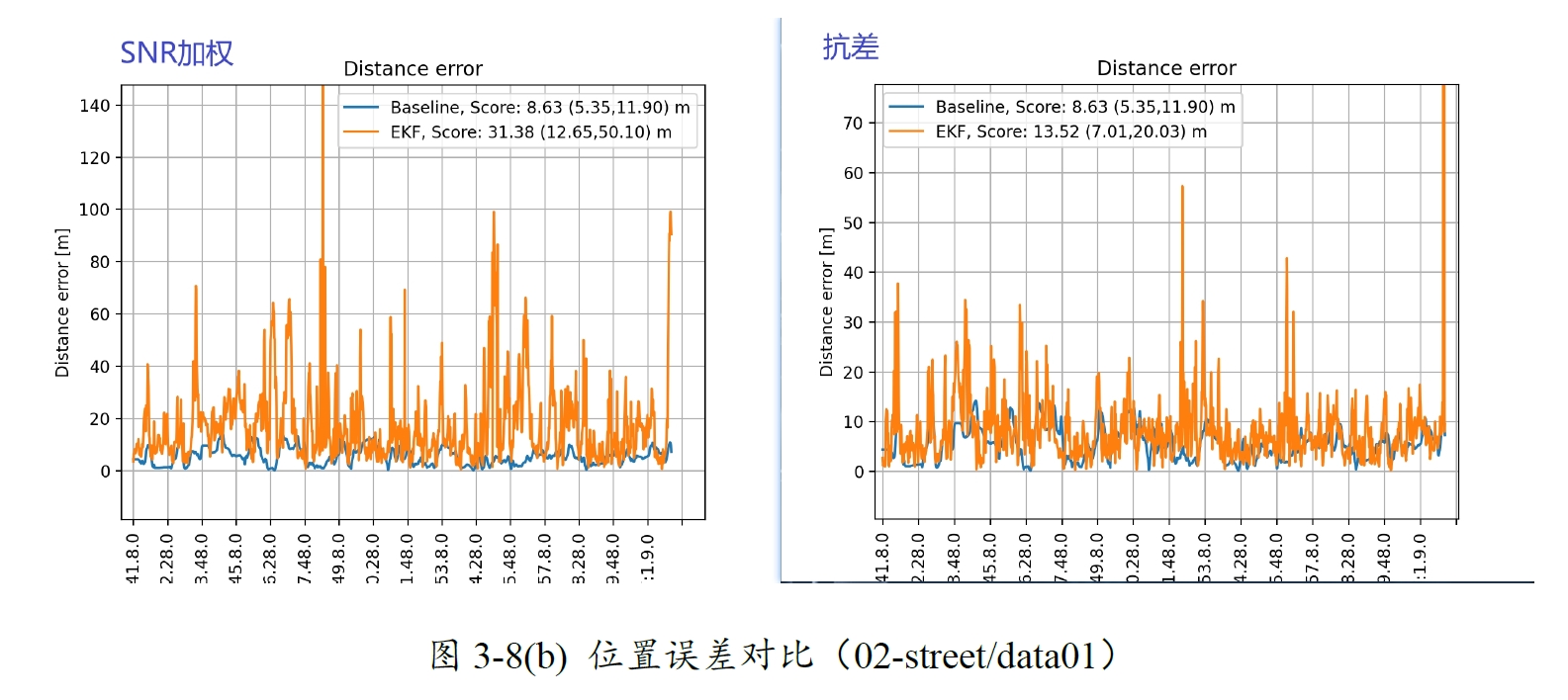
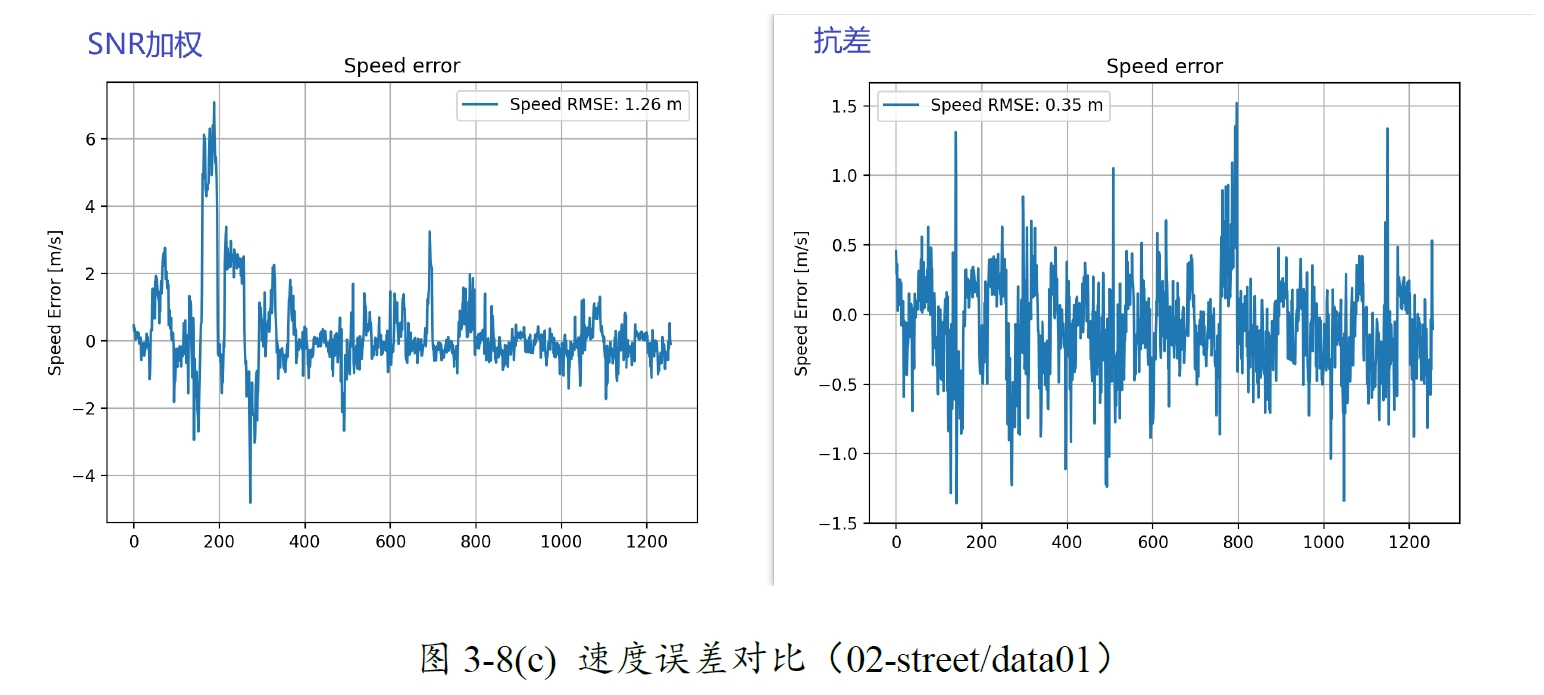
图3-8 SNR加权与Huber抗差对比（02-street/data01）

以02-street/data01组别数据为例，抗差后的结果所表现的性能提升了很多。