附录E1. 模型与算法（E.6-E.8）

该附录简要描述了RTKLIB中涉及的模型和算法（E.6-E.8）。

E.6 单点定位

RTKLIB采用迭代加权最小二乘法（LSE）用于“Single”（单点定位）模式（无论是否包含SBAS校正）。

6.1 线性最小二乘

假设给定测量向量，它可以被建模为一个包含未知参数向量和一个随机观测误差向量的线性方程：

最小二乘代价函数定义为观测误差的平方和：

通过使用 (E.6.1) 和 (E.6.2) ，代价函数可以重写为（计算时注意代价值为标量，而标量的转置为自身）：

为了最小化代价函数，的梯度应该为零。然后

这就是最小二乘法的“正规方程”（Normal Equation）：

为了解正规方程，我们可以通过最小二乘法得到估计的未知参数向量：

如果给定了每个测量的权重，可以使用权重矩阵重写代价函数 (E.6.3) 。

为了最小化代价函数，我们可以通过加权最小二乘法（WLS）以类似最小二乘法原本的方式获得估计的未知参数向量：

加权最小二乘法（WLS）的权重矩阵通常定义为：

其中是第个观测误差的先验标准差。

6.2 高斯-牛顿迭代

如果观测值不是以线性模型给出的，测量方程可以由一个通用的非线性向量函数表示为：

其中是参数向量的测量向量函数。该方程可以通过在初始参数向量处使用泰勒（级数）展开：

其中是关于在处的偏导数矩阵：

假设初始参数足够接近真实值，并且忽略泰勒级数的高阶项（第二项及其后续项）。我们可以将 (E.6.9) 近似为：

然后可以得到以下线性方程：

通过将线性加权最小二乘法 (E.6.8) 应用于 (E.6.13) ，我们可以得到非线性加权最小二乘法的正规方程：

因此，我们可以通过以下方式获得估计的未知参数向量：

如果初始参数不够接近真实值，我们可以迭代改进估计参数如下：

如果迭代收敛，我们可以得到最终的估计参数为：

迭代最小二乘法通常被称为高斯-牛顿法。请注意，对于具有较大非线性的病态（ill-conditioned）测量方程，简单的高斯-牛顿方法并不总是能够收敛。在这种情况下，我们应该采用另一种策略来处理这种非线性最小二乘问题。对于非线性最小二乘法，最流行的方法是非线性最小二乘的LM（Levenberg-Marquardt）方法。

6.3. 接收机位置和钟差估计

如果定位模式 (Positioning Mode) 设置为 “Single” ，将会通过以下单点定位过程，通过逐历元的方式获得最终解。对于一个历元时间，未知参数向量 定义为：

伪距测量向量 可以表示为：

其中 是伪距测量。如果配置选项"Ionosphere Correction"设置为"Iono-Free LC"，则使用附录 E.5(5.7) 中定义的无电离层组合（线性组合）伪距。其他情况下，则仅使用 伪距。

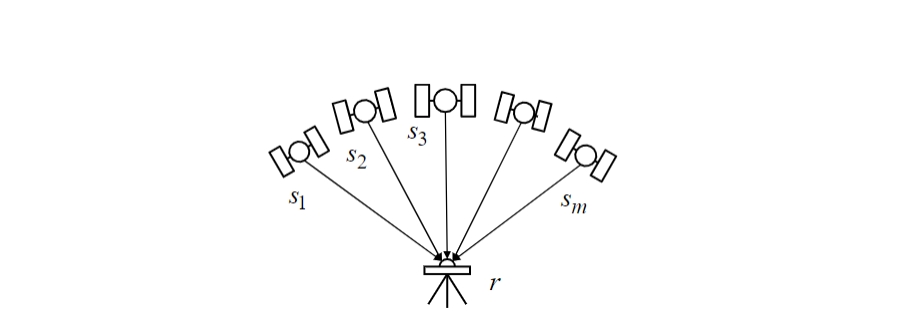
图E.6-1 单点定位的卫星几何结构

单点定位的测量方程及其偏导数矩阵构成如下：

其中几何距离 和视距（LOS）向量 由 E.3 (3.4) 和 E.3 (3.5) 给出，结合卫星和接收机的位置。卫星位置 和钟差 则根据配置选项“Satellite Ephemeris/Clock”从 E.4 中描述的GNSS卫星星历和时钟推导而来。

为了求解测量方程以获得接收机位置和接收机钟差，RTKLIB采用了迭代加权最小二乘法（LSE），如下所示：

对于迭代加权最小二乘法的初始参数向量 ，在单点定位的第一个历元中可以全部设置为0。一旦获得解，该位置将用于下一个历元接收机位置的迭代初值。对于权重矩阵 ，RTKLIB使用以下公式：

其中：

：卫星系统误差因子
（1: GPS, Galileo, QZSS和Beidou, 1.5: GLONASS, 3.0: SBAS）
：码/载波相位误差比率，伪距定位和载波相位定位使用的是同样的加权公式，这里以载波相位为基础，然后通过系数转换到了伪距上
：载波相位误差因子 和 （m）
：星历和钟差标准差（m）
：电离层校正模型误差标准差（m）
：对流层校正模型误差标准差（m）
：码偏差误差标准差（m）

手册与代码中权计算的差异

RTKLIB代码中是这样的：

// var = fact^2*R^2*(a^2 + (b^2/sin(el) + c^2*(10^(0.1*(snr_max-snr_rover)))) + (d*rcv_std)^2)

注意，这里的和都需要带上平方，手册中并没有很好的说明这一点，另外代码中还包含SNR的部分。

对于星历和钟差的标准差，RTKLIB中使用了URA（用户测距精度）或类似的指标。通过几次迭代，通常情况下解会收敛，并获得估计的接收机位置 和接收机钟差 。

估计的接收机钟差 没有明确输出到结果文件中。它被合并在定位解的时间标签中。这意味着定位解的时间标签表示的并不是接收机的时间标签，而是GPST中测量到的真实信号接收时间（包含钟差修正的观测时间）。

6.4 接收机速度和钟漂估计

如果给出了多普勒频率观测值，可以按照以下过程估计接收机速度和钟漂。对于一个历元时间，速度估计的未知参数向量 定义为：

其中 和 分别是接收机在ECEF（地心地固）坐标系中的速度（m/s）和接收机钟漂（s/s）。相应的速率测量向量 可以表示为：

其中 是卫星 的 多普勒频率观测值。

Q1：多普勒观测值的正负

RINEX 中的多普勒观测值 可以表示为：

根据多普勒效应的物理定义：

• 当接收机和卫星靠近时， ， ，多普勒记录为正值。
• 当接收机和卫星远离时， ， ，多普勒记录为负值。

绝大部分接收机满足上述规律，可以通过查看观测文件中前后两个历元的伪距或载波相位是增加还是减小来判断多普勒的符号定义。

RTKLIB总是使用 频段的多普勒频率观测值。这些测量方程及其偏导数矩阵构成如下：

这些方程中卫星相对于接收机的速度 从以下公式推导：

其中 ， 。通过使用与位置估计类似的迭代最小二乘法，我们可以获得接收机的速度和钟漂：

其中权重矩阵 设置为 （非加权最小二乘法）。

6.5 解的验证与RAIM FDE

6.3中描述的接收机位置估计可能由于未建模的观测误差而产生无效解。为了检验结果是否有效并防止无效解，RTKLIB在完成位置估计后可以采用以下验证方式。如果验证失败，将发出警告信息并拒绝该解。

其中 是待估参数的数目， 是观测量的数目。 是自由度 和 的卡方分布。GDOP是几何精度因子（dilution of precision）。 ，可以配置选项“Reject Threshold of GDOP”中进行相关设置。

除了上述解的检验之外，RTKLIB在版本2.4.2中还增加了RAIM（接收机自主完好性监控）FDE（故障检测与排除）功能。如果启用了配置选项“RAIM FDE”，那么在式(E.6.33)中的卡方检验失败后，RTKLIB将通过逐个排除可见卫星来进行重新估计。在重新进行了所有尝试后，选择具有最小归一化平方残差 的估计位置作为最终解。在这种方案中，由于卫星故障、接收机故障或较严重的多路径所导致的无效观测值将被视为异常值并被剔除掉。请注意，此功能需要2颗冗余的可见卫星，这意味着至少需要6颗可见卫星才能获得最终解。

E.7 Kinematic, Static 与 Moving-Baseline

RTKLIB在DGPS/DGNSS、Static、Kinematic、Moving-Base工作模式下采用了扩展卡尔曼滤波（EKF），同时也使用了附录E.3中的GNSS信号观测模型以及附录E.5中的对流层和电离层模型。

7.1 EKF公式

EKF量测更新。EKF在 时刻（历元时间）通过观测向量 估计未知模型参数的状态向量 及其协方差矩阵 ：

其中 和 是历元时间的 估计状态向量和其协方差矩阵。 和 表示EKF量测更新之前（先验）和之后（后验）。 ， 和 分别是观测模型向量、偏导数矩阵（雅可比矩阵）和观测误差协方差矩阵。

EKF时间更新。假设系统模型是线性的，EKF的状态向量及其协方差矩阵的时间更新可以表示为：

其中 和 是从历元时间 到 的系统状态转移矩阵和系统噪声协方差矩阵。

7.2 双差观测模型

对于短基线（<10公里）的 RTK 场景，通常使用以下双差（DD）观测方程来处理 的相位差和伪距差。在这些方程中，通过使用双差技术，卫星和接收机的钟差、电离层与对流层影响以及其他次要修正项几乎被完全消除。

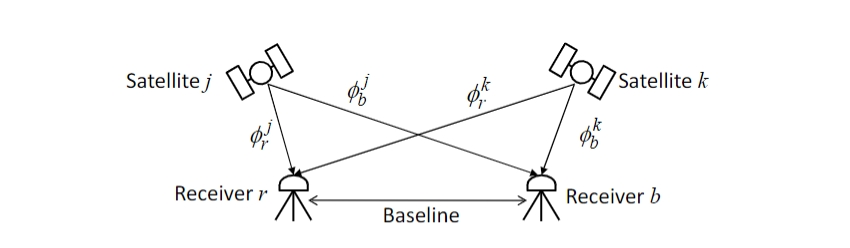
图E.7-1 双差模型

其中 是载波相位修正项，在短基线情况下可以忽略，除了 PCV项 （因使用不同接收机天线所导致）。为了在方程中获得几何距离 ，基站位置 需要设置为固定值，除非工作模式为动基线模式（Moving-Base）。

需要注意的是，接收机之间的单差（SD）最好在有相同历元时间的观测量之间进行。然而由于不同的接收机钟差，接收机并不能完全同步。在一些典型情况下，流动站的采样间隔与基站不同，例如很多流动站接收机支持1~10 Hz。RTKLIB在处理单差时，会选择在流动站历元时间之前或等于该历元时间的最后一个基站观测量。流动站和基站之间的历元时间差可以称为差分龄期（Age of Differential），相关的配置选项为“MAX Age of Diff”。随着差分龄期的增加，由于卫星钟漂和电离层延迟，解的精度会逐渐降低。RTKLIB使用广播星历种的的卫星时钟参数对单差观测量中的卫星钟漂进行修正。

至于卫星间单差（也即流动站双差），RTKLIB在每个历元的基础上选择一个具有最大仰角的参考卫星。请注意，不同导航系统之间的卫星会单独进行卫星单差的运算，这是因为即使不同导航系统的信号具有相同的载波频率，接收机通常对这些信号有不同的接收机群延迟ISB（inter system bias）。

假设流动站和基站均使用三频GPS/GNSS接收机，待估计的未知状态向量 可定义为：

其中 是 单差（SD）载波相位模糊度（cycle）。在RTKLIB的实现中，它内部使用SD载波相位模糊度而非双差（DD），主要是为了避免参考卫星切换所造成的麻烦。SD模糊度还有助于解决GLONASS FDMA信号中的整周模糊度。

观测向量 中包含了双差相位和双差伪距观测值：

其中：

7.3 EKF量测更新

通过式(E.7.6)，观测模型向量 、偏导数矩阵 （雅可比矩阵）和观测误差协方差矩阵 可以表示为：

其中：

： SD (单差) 矩阵

： 相位差观测误差的标准差（m）
： 伪距观测误差的标准差（m）

通过求解式(E.7.1)中的量测更新，可以获得 时刻估计的流动站天线位置、速度和浮点单差（载波相位）模糊度。

7.4 EKF时间更新

在RTKLIB中，设置了接收机动态的 Kinematic 模式（Positioning Mode = Kinematic， REC Dynamics = ON），EKF的时间更新（E.7.2）表示为：

其中：

是GPS/GNSS接收机采样间隔（s）， 是流动站速度噪声的东西、南北、垂直分量的标准差（m/s/√s）。

对于不考虑接收机动态的 Kinematic 模式（Positioning Mode = Kinematic, REC Dynamics = OFF），方程(E.7.9)被替换为：

为了避免因将无限大的过程噪声添加到接收机位置的方差而导致数值不稳定，接收机位置状态在每个历元被重置为初始猜测值，并在 RTKLIB 中添加了足够大的过程噪声（）。初始位置来源于单点定位，这用于避免非线性测量模型的迭代（如果没有设置初始位置，并且位置方差设置无穷大，就要靠量测更新多次迭代算出一个位置初值）。

在 Static 模式（Positioning Mode = Static）中，方程(E.7.10)被简单地替换为：

在 Instantaneous 糊度解算模式（nteger Ambiguity Resolution = Instantaneous）下，单差载波相位模糊度 的时间更新处理方式与上述略有不同。在这种模式下，载波相位模糊度状态的值不会通过EKF时间更新传递到下一个历元。模糊度在每个历元被重置为初始猜测值，并且在方差中添加了足够大的过程噪声（）。如果在测量数据中检测到周跳，相应的单差载波相位模糊度状态也会被重置为初始值。RTKLIB通过输入测量数据中的LLI（失锁指示）和双频测量的几何无关LC（线性组合）相位来探测周跳。周跳阈值可以通过配置选项“Slip Thres”来更改。

7.5 整周模糊度解算

EKF量测更新获得估计状态后，浮点载波相位模糊度（简称浮点模糊度）可以被解算为整数值，以提高精度和收敛速度。目前相关的配置选项是Integer Ambiguity Res，它可以设置为Continuous, Instantaneous 或 Fix and Hold 模式。首先，估计状态（单差和位置）及其协方差矩阵通过以下方式转换为双差（DD）形式：

其中：

： SD-DD 转换矩阵

在这个转换过程中，单差载波相位模糊度被转换为双差形式，以消除接收机初始相位项（initial phase terms），从而获得整数模糊度 及其协方差 。

“单差转双差以消除接收机初始相位项”的含义

载波相位测量值不仅包含几何距离、模糊度和钟差，还包括接收机硬件引入的初始相位偏差（Initial Phase Bias）。这是由于接收机的本地振荡器（Local Oscillator）在测量载波相位时有一个未知的起始相位。它应该可以被吸收到接收机钟差项中。

单差能消除卫星钟差和短基线情形下的大部分大气延时误差，而单差转双差我们更关心的是它能进一步消除掉接收机钟差。

在上述公式中，通过求解一个整数最小二乘（ILS）问题，可以得到最合适的整数模糊度向量 ，该问题表示为：

其中， 表示整数集。

为了解决 ILS 问题， RTKLIB 采用了一种高效且应用广泛的搜索策略 LAMBDA [66]及其扩展 MLAMBDA [67]。 LAMBDA 和 MLAMBDA 提供了线性变换和变换空间中进行树搜索的组合，从而缩小整数向量搜索空间。

解算得到的整数向量解通过以下简单的“Ratio-Test”进行验证。在“Ratio-Test”中，比率因子 定义为次优解 的加权残差平方和最优 的加权残差平方和的比值，用于检查解的可靠性。验证阈值 可以通过配置选项“Min Ratio to Fix Ambiguity”进行设置。原始版本的 RTKLIB 仅支持固定的阈值，而在 demo5 改进版本中，能够支持自适应 Ratio 。

验证通过后，Rover的固定（FIX）解 和 通过求解以下方程获得。如果验证失败，RTKLIB 则输出浮点（FLOAT）解 和 代替。

如果配置选项设置为“Fix and Hold”模式（Integer Ambiguity Res = Fix and Hold），并且固定解通过之前的验证通过，则双差载波相位模糊度参数会被严格约束到固定的整数值。为此，RTKLIB 会输入以下“伪（pseudo"）”观测值到 EKF，并通过公式 (E.7.1) 更新 EKF：

其中：

：SD to DD 转换矩阵

: 约束到固定的整数模糊度误差（≈ 0.001 cycle）

“Fix and Hold”模式最初在 RTKLIB 2.4.0 版本中引入，它能显著提高接收机在运动状态下的固定率。

7.6 长基线双差观测模型

对于接收机r和基站b之间的长基线处理，可以形成类似于短基线双差（DD）模型的以下双差测量方程：

其中和作为电离层延迟（米）和对流层延迟（米）被添加到短基线双差模型中。对于超过100公里的基线，应使用精确的星历书来减轻广播星历误差。在载波相位修正项中，对于超过500公里的基线应考虑地球潮效应。为了消除电离层项，有时会形成无电离层LC（线性组合）。然而，RTKLIB不使用这种显式LC，而是通过EKF直接估计基线处理的双频或三频测量的电离层项。

长基线情况下的未知状态向量 也可以设定为：

其中 和 是 ZTD（zenith total delay）在Rover和基站位置的值，、、 和 是对流层梯度的北向和东向分量。 是 频率（）下的SD垂直电离层延迟。

观测模型向量 和偏导数矩阵 可以表示为：

其中：

对于长基线情况，EKF 的时间更新表达式为：

其中，和分别为电离层和对流层项的过程噪声协方差矩阵。在该方程中，Rover和基站的ZTD（天顶总延迟）及梯度参数，以及每颗卫星的SD（单差）垂直电离层延迟，均被简单地建模为随机游走过程。此外，为了估计电离层和对流层项，在2.4.1版本中为长基线处理增加了一个“部分固定”功能。这意味着只有部分模糊度被解算为整数值，其余未固定的模糊度仍保持为浮点值。为了确定模糊度是否固定，RTKLIB中实现了一个使用卫星仰角的简单标准。如果卫星的仰角低于设定的阈值，则该卫星的模糊度不会被固定。只有仰角高于阈值的卫星的模糊度才会被解算为整数。模糊度解算的仰角阈值可以通过配置选项“最小仰角固定模糊度”（Min Elevation to Fix Amb）以及“最小仰角保持模糊度”（Min Elevation to Hold Amb）来设置，以控制“固定和保持”（Fix and Hold）功能。

7.7 动态基线模型

移动基线模式通常在Rover和基站接收器都在移动且仅需要Rover相对于基站的相对位置时使用。通过在移动平台上安装两个天线，可以利用移动基线模式确定精确姿态。在 RTKLIB 中，如果将配置选项“定位模式”设置为“移动基线”，则应用移动基线模式。

在移动基线模式下，基站位置不是固定的，而是通过逐历元的单点定位过程估计的。一旦获得基站位置，将基站位置固定为估计位置，并通过 (1)-(5) 中描述的短基线运动模式估计Rover位置。在这种情况下，只有相对位置是有意义的，也就是说，Rover和基站的绝对位置解的精度仅与点定位模式的解相同。

除了对移动基线模式的简单实现外，RTKLIB 还校正了Rover与基站之间的时间差异。Rover接收机和基站接收机不同步。接收机时钟差通常最大可达 2 毫秒。对于非常快速移动的平台，不同步的时钟会导致精度下降。为了校正时钟差，在基线处理之前，基站位置通过以下公式进行校正：

其中，和 分别是通过单点定位过程估计的Rover和基站的信号接收时间。也是通过多普勒测量估计的基站速度。对于通过移动基线模式进行姿态确定的情况，如果启用配置选项“基线长度约束”（Baseline Length Constraint），则可以应用基线长度约束。该约束在 EKF 量测更新中应用以下伪测量：

其中， 是给定的预设基线长度（单位：米），是基线长度的约束（单位：米）。为了应对非常短的基线长度情况下的非线性问题，可以通过将配置选项“滤波器迭代次数”（Number of Filter Iteration）设置为大于1，来支持扩展卡尔曼滤波器（EKF）的迭代量测更新。

E.8 PPP

TBD