附录E1. 模型与算法（E.1-E.5）

该附录简要描述了RTKLIB中涉及的模型和算法（E.1-E.5）。附录中使用的常见模型或方程的缩写如下所示。

: 光速 (m/s)
: 频段伪距 (m)
: 频段多普勒频率 (Hz)
: 频段载波相位 (cycle)
: 频段载波相位 (m)
: 导航信号发送至接收机时间，即接收机收到信号的时间 (s)
: 卫星发送导航信号时间 (s)
: 卫星和接收机天线之间的几何距离 (m)
: 卫星和接收机天线之间的伪距率 (m/s)
：t时刻ECEF下卫星位置（m）
：t时刻ECEF下卫星速度(m/s)
：t时刻ECEF下接收机天线位置（m）
：t时刻ECEF下接收机天线速度（m/s）
：ECEF下，接收机到卫星的LOS单位向量
：当地坐标系下，接收机到卫星的单位向量
：ECEF坐标系到大地坐标系的旋转变换矩阵
：ECEF坐标系到卫星载体坐标系的旋转变换矩阵
：接收机天线位置的纬度/大地维度
：接收机天线位置的经度/大地经度
：当前位置观测，卫星的方位角（rad）
：当前位置观测，卫星的高度角（rad）
：t时刻接收机钟差（s）
：t时刻接收机钟漂——频差（s/s）
：t时刻卫星钟差（s）
：t时刻卫星钟漂——频差（s/s）
：对流层延迟（m）
：L频段电离层延迟（m）
：频段载波频率（Hz）
：频段波长（m）
：L频段载波偏差（cycle）
：L频段载波整周模糊度（cycle）
：伪距测量误差（m）
：载波相位测量误差（cycle）
：载波相位测量误差（m）
：地球自转角速度（rad/s）
：当地坐标系下，L频段接收机天线相位中心偏差(PCO)（m）
：卫星载体坐标系下，卫星天线L波段相位中心偏差(PCO)（m）
：频段接收机天线相位中心变化PCV（m）
：频段卫星天线相位中心变化PCV（m）
：接收机天线到卫星的天底角（）
：当地坐标系下，接收机天线位置处的地球潮偏移
：相位缠绕效应（cycle）
：卫星时钟的相对论改正/Trel
：t时刻ECI和ECEF的坐标系转换矩阵
：绕X轴旋转θ得到的坐标旋转矩阵
：绕Y轴旋转θ得到的坐标旋转矩阵
：绕Z轴旋转θ得到的坐标旋转矩阵
：卫星端，卫星j和k之间的单差
：地面端，基准站b和移动站/r之间的单差
：对流层天顶总延迟（m）
：对流层天顶干延迟（m）
：对流层东向梯度分量
：对流层北向梯度分量
：天顶对流层干延迟映射函数
：天顶对流层湿延迟映射函数
：电离层延迟映射函数

E.1 时间系统

RTKLIB内部采用GPS时间进行GNSS数据处理和定位；UTC时间（协调世界时）是一个不连续时间，简而言之，它和GPS时间之间存在一个跳秒（或闰秒）的关系。GPS时间通常采用周数和周内秒来表示其起始历元为1980年1月6日00:00:00 UTC。但是对于double类型变量来说，其距离精度只有0.04米。因此，在实际运算时，RTKLIB调用C标准库中的时间结构体并定义了gtime_t类型：

typedef struct {
    time_t time; /* time (s) expressed by standard time_t */
    double sec;  /* fraction of second under 1 s */
} gtime_t;

time_t 通常通过一个无符号的32位整数来实现，表示从1970年1月1日00:00:00开始的总秒数。由于整数位的长度限制，，gtime_t 无法处理1970年1月1日之前或2038年1月19日之后的时间。

gtime_t 中的sec字段用于存储小数秒。sec在距离上的分辨率为6.7×10⁻⁸米，足以满足GNSS高精度定位计算的需求。RTKLIB还提供了几个有用的API来处理gtime_t，包括加、减以及时间格式的转换。

不同导航系统的时间定义有所差异，以下是所有时间系统特性的汇总。

表E.1-1 时间系统汇总

时间系统	连续性	起始历元	与UTC的关系	转换公式
GPST	连续	1980年1月6日00:00:00 UTC	UTC比GPST慢，差值为累积的闰秒数（ΔtLS）	tUTC=tGPST-ΔtLS
GLONASST	不连续	与UTC（SU）对齐	UTC比GLONASST慢3小时，差值为固定偏移和闰秒数	tUTC=tGLONSASST-10800
GST	连续	1999年8月22日00:00:00 UTC	GST比UTC快13秒，与GPST对齐，但有1024周的差异和小时间偏移（GGTO）	无直接公式，需考虑与GPST的对齐关系
QZSST	连续	与GPST对齐	QZSST与GPST具有相同的起始点和秒定义	无直接公式，可直接处理为GPST
BDT	连续	2006年1月1日00:00:00 UTC	BDT比UTC快14秒，时间差被控制在100纳秒以内（模1秒）	tBDT=tGPST-14

1. GPST（GPS时间）和UTC（协调世界时）

现在的UTC时间比GPST慢，因为它当前闰掉的时间为负数。GPST与UTC（协调世界时）之间的粗略转换可以简单地表示为：

其中，和分别是以秒为单位的UTC时间和GPS时间。是由于自1980年1月6日以来累积的闰秒（或跳秒）导致的UTC与GPST之间的时间差（秒）。的值如表E.1-1所示。

表E.1-2 GPST-UTC值（截至2025年2月）

Time Since (in UTC)     𝛥𝑡𝐿𝑆 (s)
-----------------------------
1980-01-06 00:00:00       0
1981-07-01 00:00:00       1
1982-07-01 00:00:00       2
1983-07-01 00:00:00       3
1987-01-01 00:00:00       4
1988-01-01 00:00:00       5
1990-01-01 00:00:00       6
1991-01-01 00:00:00       7
1992-07-01 00:00:00       8
1993-07-01 00:00:00       9
1994-07-01 00:00:00      10
1996-01-01 00:00:00      11
1999-01-01 00:00:00      13
1997-07-01 00:00:00      12
2006-01-01 00:00:00      14
2009-01-01 00:00:00      15
2012-07-01 00:00:00      16
2015-07-01 00:00:00      17
2017-01-01 00:00:00      18

公式（E.1.1）或（E.1.2）的近似精度在几十纳秒以内。通过使用GPS导航消息中的UTC参数，我们可以更精确地将GPST与UTC之间的转换，公式如下：

其中，、、、、和是GPS导航消息中提供的UTC参数。更严格地说，公式（E.1.3）中的UTC是UTC(USNO)，即美国本地实现的UTC。UTC与UTC(USNO)之间的差异可以在BIPM提供的T公报中获得，这种差异通常在纳秒级别。

2. GLONASST (GLONASS时间)

GLONASST（GLONASS时间）基于UTC（SU），因此它同样包含了闰秒。GLONASST还与当地时间对齐。因此，大致上，GLONASST中的时间可以转换为UTC中的时间。

更准确地说，GLONASS导航信息中的GLONASST的UTC参数应类似于GPST（GPS时间）和UTC转换的方式使用。忽略闰秒和3小时的时差，GPST与GLONASST之间的差异通常为100纳秒或几个100纳秒的水平。

3. GST (Galileo时间)

伽利略系统时间（Galileo System Time，GST）与GPST类似，同样有周与周内秒组成。GST的起始历元为1999年8月22日00:00:00 UTC（这个时间刚好和GPS的起始时间1980年1月6日00:00:00 UTC相隔1024周）。在起始历元时，GST比UTC快13秒。GST是连续时间，不插入或删除闰秒。因此，GST与GPS时间（GPST）对齐，除了时间系统原点的1024周差异和一个小的时间偏移（Galileo/GPS时间差异，GGTO）。根据RINEX约定，伽利略周数与GPS周数相等。

4. QZSST (QZSS时间)

QZSST（QZSS时间）与GPST（GPS时间）对齐。它与GPST具有相同的起始点和相同的秒定义，QZSST可以像GPST一样处理。

5. BDT (北斗时间)

北斗时间（BDT）也是一个连续时间系统（没有闰秒的插入或删除）。BDT的起始历元为2006年1月1日00:00:00 UTC。BDT与UTC之间的时间差被控制在100纳秒以内（模1秒）。因此，GPS时间（GPST）中的时间可以大致通过以下公式转换为BDT中的时间，精度约为200纳秒：

BDT同样需要使用北斗导航信息中的UTC参数，然后进行类似GPST与UTC之间的转换。

Q1：为什么使用double类型表示GPS时间，距离精度是0.04米？

首先搞清楚要干嘛。这里是想说明以double类型来表示GPS时间，数值精度会很低。我们可以进行如下分析：

1. double 类型的精度

• double 类型是 64 位浮点数，遵循 IEEE 754 标准。
• 其尾数部分有 52 位，因此精度为：
  

2. GPS 时间的表示

• GPS 时间通常以周数（week）和周内秒（second of week）表示。
• 一周的总秒数为：
  604800s (7天×86400s/天)
• 用 double 类型表示 GPS 时间时，其最小分辨率为：
  

3. 时间分辨率转换为距离误差

• 光速 c 为：
  
• 时间分辨率对应的距离误差为（使用 double 类型表示 GPST 时的最小分辨率）：
  
• 如果用double类型表示一个比604800更大的数值时候，距离误差还会比0.04m更大（当时间需要参与运算时，要考虑这个误差的；当时间只是用来标识与显示时，则可以不用管这个误差）。

E.2 坐标系统

在RTKLIB中，接收机和卫星的位置以ECEF（地心地固坐标系）的X、Y、Z分量表示。ECEF框架的选择取决于卫星星历和基准站位置，并未明确固定。例如，使用GPS信号时，单点定位结果通常基于WGS84坐标系。在基线分析中，移动站的位置会被转换到与基准站相同的ECEF框架中。实际上，常用的ECEF框架（如WGS84、PZ90.02和ITRF）在广播星历或单点定位精度范围内是等效的。然而，对于基线分析或PPP（精密单点定位），需要更严格地处理坐标系，使用统一的坐标系可以有效减少处理误差。

(1) 从大地坐标转换为ECEF XYZ坐标 大地坐标是基于参考椭球体定义的，如图E.2-1所示。大地纬度、经度和椭球高可以转换为ECEF XYZ坐标，转换公式如下：

其中，
：地球参考椭球体的长半轴（米）
：地球参考椭球体的扁率

当前版本的RTKLIB始终使用WGS84坐标系提供的参考椭球体的和值如下：

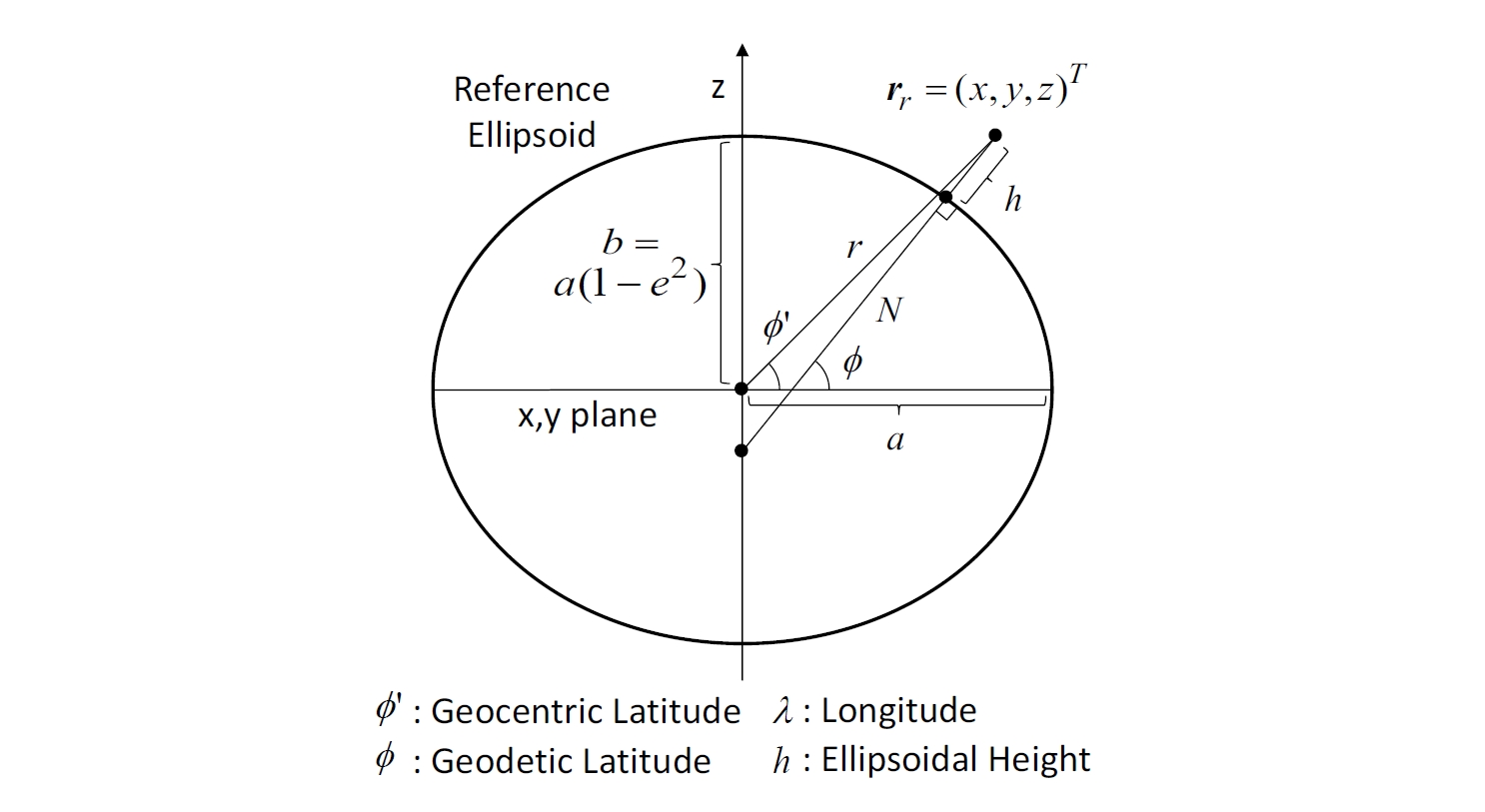
图E.2-1 参考椭球体

(2) 将ECEF坐标转换为大地坐标 将ECEF中的XYZ位置 转换为大地坐标，需采用以下步骤。在此过程中，大地纬度是通过迭代方法计算得出的。

(3) 本地坐标与ECEF坐标之间的转换 接收机位置的局部坐标（也称为ENU坐标）在GNSS导航处理中经常被使用。从ECEF坐标到局部坐标的旋转矩阵 ​ 表示为：

其中，和分别是接收机位置的大地纬度和经度。通过使用旋转矩阵以及接收机在ECEF坐标系中的位置，可以将ECEF坐标系中的位置转换为局部坐标系中的位置，转换公式如下：

(4) 似大地水准面模型 为了从椭球高得到大地高，我们需要考虑似大地水准面高。大地高 hgeod​（单位：米）表示为：

其中， 是在纬度 和经度 ​ 处的似大地水准面高（单位：米）。RTKLIB支持通过处理选项“似大地水准面模型”选择以下几种似大地水准面模型。所有这些模型均以纬度和经度网格点上的似大地水准面高提供。RTKLIB使用双线性插值来获取适用于特定纬度和经度位置的值。除了内部模型外，使用这些似大地水准面模型时，需要下载相应的似大地水准面数据文件，并将其文件路径设置为处理选项“似大地水准面数据文件”。

(a) 内置模型：基于EGM96的1度×1度网格似大地水准面模型 (b) EGM96：15" x 15" 网格的EGM96似大地水准面模型 (c) EGM2008：2.5" x 2.5" 网格或1弧秒×1弧秒网格的EGM2008似大地水准面模型 (d) GSI 2000：1" x 1.5" 弧秒网格的GSI 2000似大地水准面模型（仅适用于日本列岛周边）

E.3 GNSS信号测量模型

3.1 GNSS信号结构

图E.3-1展示了一个典型的GNSS信号结构。GNSS信号通常由载波（Carrier）、伪码（Code）和导航数据码（Data）的乘积组成。具体的，伪码和数据码一起先通过调制而依附在正弦波形式的载波上，然后卫星将调制后的载波信号播发出去。

GPS、GLONASS、Galileo、QZSS、北斗和SBAS提供的GNSS信号详细规格可以在附录G中找到。

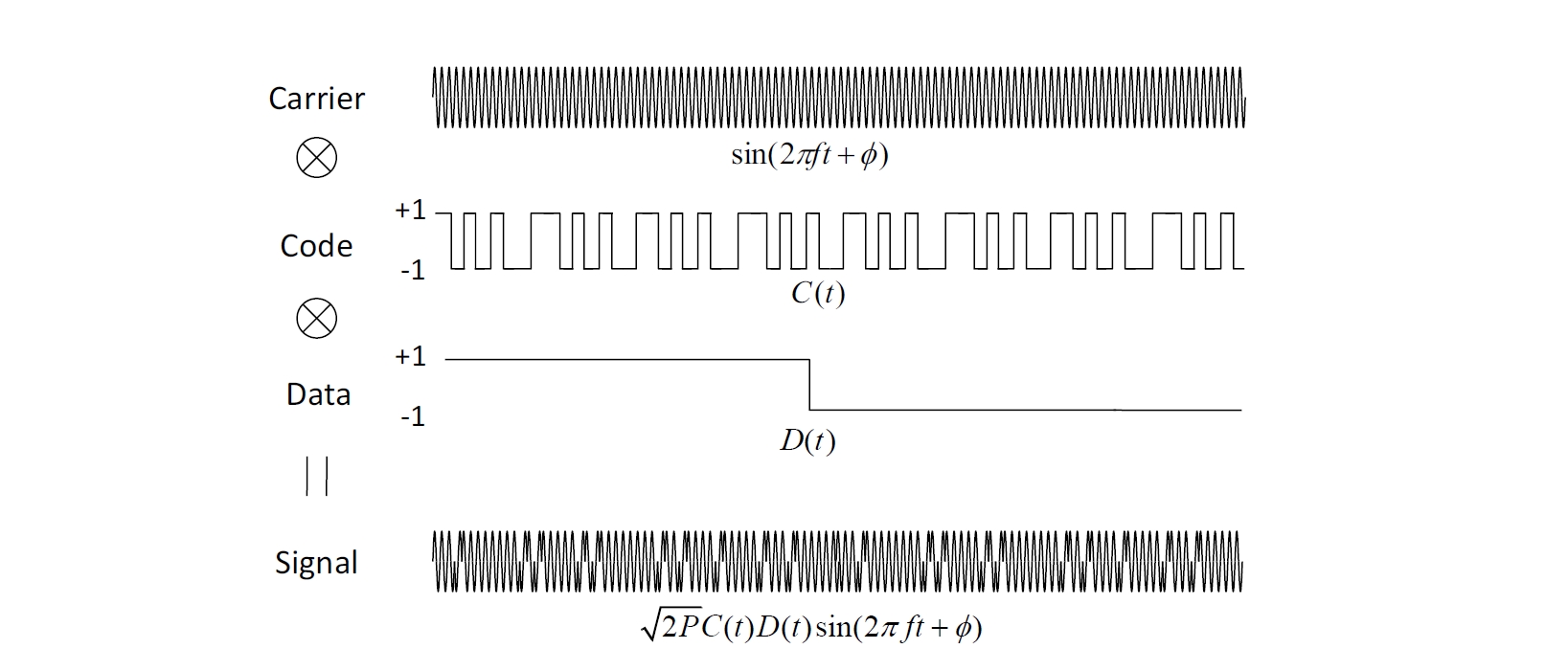
图E.3-1 GNSS信号结构

3.2 伪距测量模型

伪距指的“接收机天线到卫星天线之间的距离，其中包含了卫星钟差和接收机钟差（及其他偏差，如大气层延迟）”[9]。频段的伪距 可以用接收机测量的信号接收时间 和卫星测量的信号发射时间 来表示：

该方程也可以用卫星与接收机天线之间的几何距离 ，接收机和卫星的钟差 、，电离层和对流层延迟 、，以及测量误差 来表示：[64]

图E.3-2 伪距模型

3.3 载波相位测量模型

“载波相位其实是测量卫星发来的信号载波和接收机自己产生的参考信号之间的一种节拍差（beat frequency）”[9]。频段的载波相位 可以表示为：

其中， 是初始时间（s）， 是接收机本地振荡 频段的相位（cycle）， 是 时刻发射的导航信号的 相位（cycle）。 是接收机本地振荡器在 时刻的 初始相位（cycle）， 是 时刻发射的导航信号的 初始相位（cycle）。

相位距 定义为载波相位与载波波长 （m）的乘积，也可以通过载波相位偏差 和载波相位校正项 来表达，后者包括天线相位中心偏移和变化、地球潮汐导致的站点位移、相位缠绕效应以及卫星钟的相对论校正：

其中：

通常被称为载波相位整数模糊度、载波整周模糊度或简称为模糊度。有关载波相位校正项的详细公式，请参考附录 E.8。

GPS L1频段的载波波长是19cm，为什么通常说载波相位的测量精度是cm或mm级别？

虽然 L1 载波的波长是 19 cm，但测量精度远高于波长，这是因为载波相位测量的精度取决于相位分辨能力，而不是波长本身。

接收机的相位测量是通过接收机锁相环实现的，它能分辨非常小的相位变化，实际测量精度通常在 0.01 周期左右（即1.9mm），主要受噪声和硬件限制。

3.4 卫地距（接收机与卫星天线）

接收机与卫星天线几何距离（卫地距）指卫星天线（相位中心）与接收机天线（相位中心）在惯性坐标系中的物理距离。首先，信号传输时间 可以通过以下方式推导出来：

方程的两边都包含了 。因此，需要进行几次迭代来解这个方程。几何距离可以通过 ECEF坐标系中 时刻的接收机位置 与 时刻的卫星位置 来表示：

其中， 是 时刻从 ECEF（地心地固）到 ECI（地心惯性）坐标系的转换矩阵。为了在 ECEF 坐标系中表达几何距离，需要考虑地球自转效应以获得几何距离。该方程可以用以下方程之一近似，精度在1毫米级别以内。当前版本的 RTKLIB 使用方程 (F.3.8b) 来计算几何距离。(F.3.8b) 中的最后一项有时被称为萨格纳克效应（Sagnac effect）。

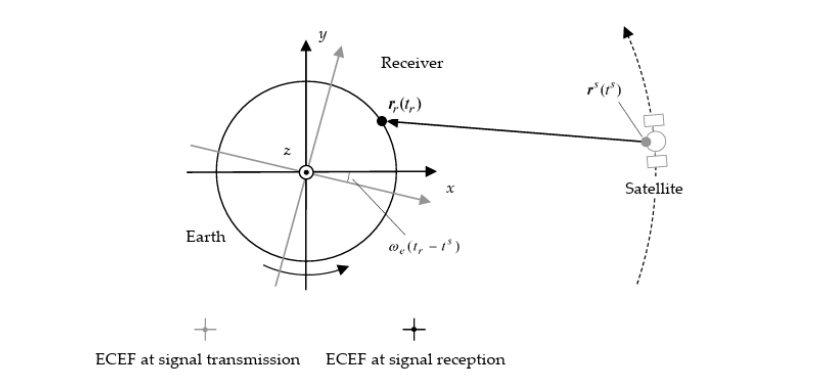
图E.3-3 几何距离和地球自转校正

3.5 卫星方位角与仰角

接收机到卫星的单位视距（LOS）向量在 ECEF（地心地固）坐标系中可以表示为：

在方程中，忽略了地球自转效应。从接收机到卫星方向的方位角 和仰角 可以从以下公式推导出来：

其中， 是从 ECEF 坐标系到接收机位置的局部坐标系的坐标旋转矩阵。有关该矩阵的详细形成，请参考 附录 E.2。

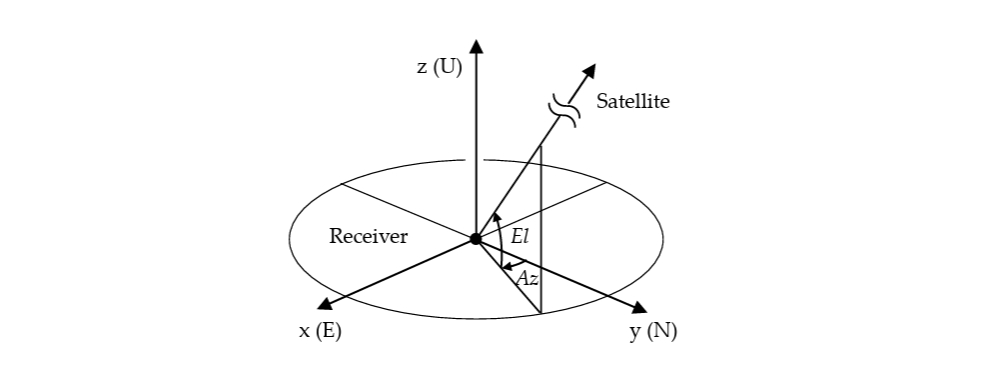
图E.3-4 局部坐标系与方位角和仰角

E.4 GNSS卫星星历与钟差

RTKLIB 支持 GPS、GLONASS、Galileo、QZSS、BeiDou 和 SBAS 的广播星历和钟差数据。它还支持作为 SP3-c 文件和钟差 RINEX 文件提供的精确星历和钟差数据，这些文件包括 Galileo、QZSS 和 BeiDou，用于后处理模式。对于实时模式，支持使用 SBAS 长期和快速修正后的广播星历和钟差数据，以及使用 RTCM 3 SSR（状态空间表示）修正的数据。以下方程展示了 RTKLIB 中使用的星历和钟差模型。

(1) GPS、Galileo 和 QZSS 的广播星历和钟差数据 [1][5][6]

GPS、Galileo 和 QZSS 的广播星历和卫星钟差参数在导航消息中给出如下：

通过使用这些参数，可以计算出卫星在 ECEF 坐标系中的位置（天线相位中心位置）、卫星钟差 和钟漂 。

其中：

: 地球引力常数（ 用于 GPS 和 QZSS， 用于 Galileo）
: 地球角速度（ rad/s）
for pseudorange
: 群延迟参数，用于 GPS 和 QZSS， for Galileo (s)

开普勒方程（E.4.4）可以通过牛顿法迭代求解。

广播星历和时钟在处理选项“Satellite Ephemeris/Clock”设置为“Broadcast”时适用，同样适用于GLONASS、BeiDou和SBAS。

2. GLONASS的广播星历和时钟 [4]

GLONASS的广播星历和时钟参数在导航消息中给出如下：

卫星位置 和速度 在地心固定坐标系（ECEF，PZ90.02）中的微分方程可以表示为：

其中：

：地球半长轴（6378136.0 m）
：地球引力常数（398600.444 × 10⁹ m³/s²）
：地球角速度（7.292115 × 10⁻⁵ rad/s）
：地球引力场的二阶球谐系数（1082625.7 × 10⁻⁹）

注意，GLONASS ICD 5.1 [4] 的 A.3.1.2 中的两个勘误已在上述模型中得到修正。

卫星位置 和速度 在时间 可以通过 RK4（Runge-Kutta 4阶和4阶段）数值积分方法求解这些微分方程，初始条件为参考时间 时的卫星位置 和速度 。对于卫星时钟偏差 和漂移 在历元时间 也同样推导如下：

卫星钟中的相对论效应已包含在GLONASS时钟参数中。因此，在此情况下不应用相对论校正。

3. 北斗卫星的广播星历和时钟 [7]

对于北斗卫星，与GPS、Galileo和QZSS相似的星历和时钟参数在导航消息中提供如下：

对于北斗的MEO和IGSO卫星，使用的公式与(1)中GPS星历和时钟相同，只是， rad/s，且时间 以BDT（北斗时间）表示。

为了在BDT（北斗时间）的时间 获取北斗GEO卫星的位置 ，应替换方程 (E.5.13) 和 (E.5.14)，具体如下：

其中：

4. SBAS的广播星历和时钟 [8]

SBAS GEO卫星的导航消息参数在SBAS消息（消息类型9）中提供如下：

通过使用这些参数，可以计算出在ECEF坐标系中的卫星位置 和卫星时钟偏差 。

5. SBAS轨道和时钟改正 [8]

SBAS轨道和时钟改正被定义为以下参数：

IOD表示目标广播星历和时钟参数。修正后的卫星位置 在时间 时计算如下：

其中：

: 由带IOD的广播星历在时间 计算的卫星位置（米）

校正后的卫星时钟偏差 在时间 时通过SSR校正计算如下：

其中：

: 由带IOD的广播时钟在时间 计算的卫星时钟偏差。

SBAS校正与广播星历和时钟结合使用的情况是在处理选项“Satellite Ephemeris/Clock”设置为“Broadcast+SBAS”时。

6. 精密星历和时钟

GPS、GLONASS、Galileo、QZSS和BeiDou的精确星历通常以SP3-c文件的形式提供，这些文件包含每15分钟或5分钟历元的卫星位置和速度（可选）。为了在时间 获得卫星位置，需要适当的插值。RTKLIB使用固定阶数（）的Newton-Neville多项式插值算法，如下所示：

其中 是插值的多项式阶数， 是历元时间 处每个组件的星历值。例如，在 的情况下，时间 处的插值值 可以推导为：

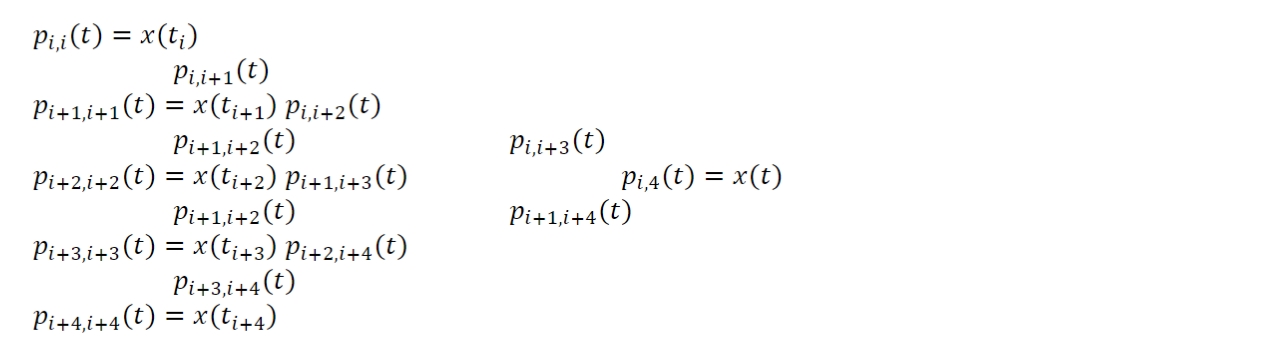
请注意，精确星历通常提供卫星的质心（CoM，中心质量）位置，而非天线相位中心位置。因此，用户应校正卫星天线相位中心偏移以使用精确星历。详情请参阅附录E.8。

尽管精确星历通常使用高阶多项式插值，但对于以SP3-c或时钟RINEX文件形式提供的精确时钟，采用了简单的线性插值，表达式如下：

对于由IGS（国际GNSS服务）提供的精确时钟，应进行相对论效应的校正：[68]

卫星时钟偏差 的相对论校正表达式如下：

其中， 和 是从精确星历推导出的卫星位置和速度。

精确星历和时钟在处理选项“Satellite Ephemeris/Clock”设置为“Precise”时适用。

IOD 表示目标广播星历和时钟参数。校正后的卫星位置 在时间 时计算如下：

其中：

: 由带IOD的广播星历在时间 计算的卫星位置（米）
: 由带IOD的广播星历在时间 计算的卫星速度（米/秒）

卫星速度 通过以下微分近似计算，其中 （秒）。

校正后的卫星时钟偏差 在时间 时通过SSR校正计算如下：

其中：

: 由带IOD的广播时钟在时间 计算的卫星时钟偏差，带有以下相对论校正：

SSR校正与广播星历和时钟结合使用的情况是在处理选项“Satellite Ephemeris/Clock”设置为“Broadcast+SSR APC”或“Broadcast+SSR CoM”时。

E.5 对流层与电离层模型

5.1. 对流层模型

标准大气可以表示为：

其中 是总压强（hPa）， 是空气的绝对温度（K）， 是大地高程（高于平均海平面，单位：m）， 是水蒸气的偏压（hPa）， 是相对湿度。对流层延迟 由Saastamoinen模型表示，基于从标准大气导出的 、 和 。

其中 是天顶角（弧度），定义为 。

标准大气和Saastamoinen模型在处理选项“Troposphere Correction”设置为“Saastamoinen”时适用，其中大地高程由椭球高程近似，且相对湿度固定为70%。

5.2 SBAS 对流层模型

如果处理选项“对流层校正”设置为“SBAS”，则应用 SBAS 接收器规范中定义的 SBAS 对流层模型。该模型常被称为“MOPS 模型”。参考 [8] A.4.2.4 获取详情。

5.3 精确对流层模型

如果处理选项“对流层校正”设置为“估计 ZTD”或“估计 ZTD+Grad”，则应用更精确的对流层模型，并使用严格的映射函数如下：

其中：

: 对流层天顶总延迟 (m)
: 对流层天顶静水延迟 (m)
: 静水映射函数
: 湿映射函数

在 RTKLIB 中，对流层天顶静水延迟由 Saastamoinen 模型（E.5.4）给出，假设天顶角 且相对湿度 。对于映射函数，RTKLIB 默认使用 Niell 映射函数（Niell mapping function）[70]。天顶总延迟 和梯度参数 、（在“估计 ZTD+Grad”情况下）作为未知参数在参数估计过程中被估算。对于映射函数，RTKLIB 自版本 2.4.2 起可以通过设置编译器选项 -DIERS_MODEL 使用 GMF [71]。

5.4 广播电离层模型

对于单频GNSS用户的电离层校正，GPS和QZSS导航数据包括以下广播电离层参数。

通过使用这些电离层参数，可以按照以下过程推导出电离层延迟（米）。该模型通常称为Klobuchar模型。

如果处理选项 "Ionosphere Correction" 设置为 "Broadcast" 或 "QZSS Broadcast"。

5.5 SBAS 电离层模型

SBAS 对电离层延迟的校正由消息类型 18（电离层网格点掩模）和消息类型 26（电离层延迟校正）提供。如果处理选项 "Ionosphere Correction" 设置为 "SBAS" 并且这些 SBAS 消息在输入文件中提供，RTKLIB 使用 SBAS 电离层校正。关于模型的算法和 IGPs（电离层网格点）的定义，请参阅 SBAS 接收器规范 [8] 的 A.4.4.9 和 A.4.4.10。

5.6 单层模型

电离层通常被建模为图 E.5-1 所示的简单单层模型。单层模型也被称为薄壳模型。

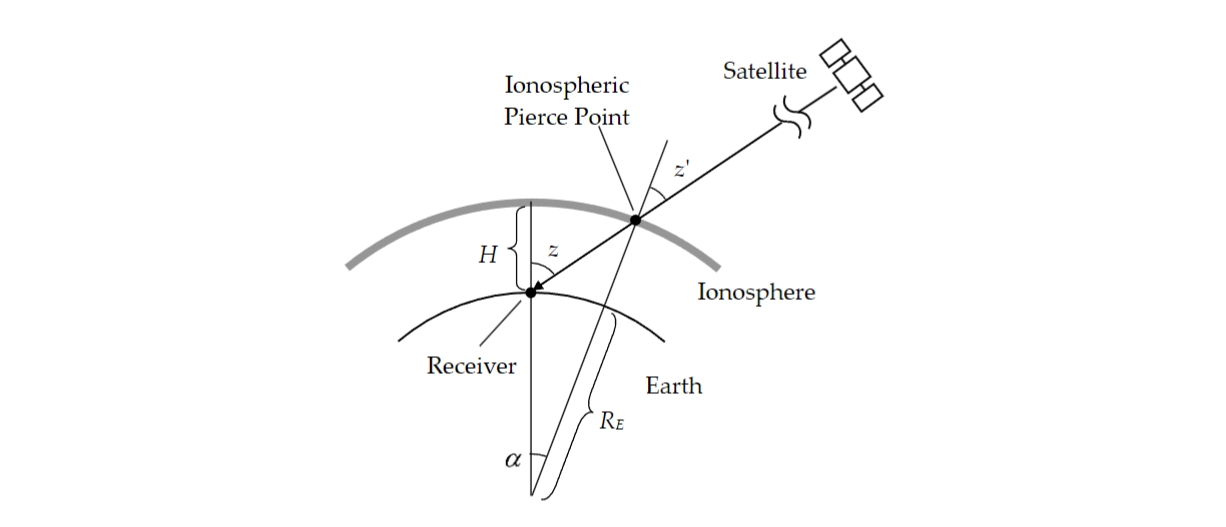
在模型中，IPP（电离层刺点）的纬度（rad）和经度（rad）可以从以下公式推导：

（ 且 ）或（ 且 ）

（否则）

其中是地球的半径（米），是电离层壳体的高度（米）。RTKLIB通常使用和。请注意，在该模型中，地球表面或电离层壳体被近似为一个球体。

如果在IPP和时间处给出了VTEC（垂直总电子含量）值，则电离层延迟$I_{r,i}^s)（米）可以表示为：

其中是信号的载波频率（Hz）。

VTEC值以几种格式或方程提供。RTKLIB目前仅支持IONEX格式提供的VTEC值。在IONEX格式中，VTEC表示为纬度和经度网格中的点值。RTKLIB通过简单的双线性插值将IONEX数据中的这些网格点值插值到合适的IPP位置。这些VTEC值在IONEX文件的每个历元时间间隔提供。时间插值也应应用于太阳固定坐标系，如下所示：

其中， 和 ( ) 是提供的TEC数据的时间， 是太阳相对于地球的旋转速度。如果处理选项 "Ionosphere Correction" 设置为 "IONEX TEC" 并且IONEX数据仅在后处理模式下作为输入文件提供，则应用单层模型和IONEX数据的校正。

5.7 无电离层组合（线性组合）

为了消除GNSS信号测量中的电离层影响，通常在GNSS数据处理中利用双频测量的LC（线性组合）。和伪距和相位差的无电离层LC表示为：

其中和是无电离层影响的LC的系数。和由以下公式导出：

其中和是和测量的频率（Hz）。当前版本的RTKLIB总是对GPS、GLONASS和QZSS使用和，对Galileo使用和进行无电离层影响的LC。如果在单一或PPP模式下将处理选项 "Ionosphere Correction" 设置为 "Iono-Free LC"，则无电离层影响的LC用于基本测量以消除电离层项。请注意，无电离层影响的LC模型不适用于Kinematic、Static或Moving-base模式。详情请参阅E.7(7.1)。